
Immaginiamo di descrivere a un amico la strada per raggiungerci in un posto sconosciuto e tramite un messaggio WhatsApp. La nostra descrizione sarà tanto più efficace quanti più punti di riferimento abbiamo in comune con lui. Potrebbe per esempio suonare così: “Dopo il supermercato gira a destra, prosegui fino alla vecchia fabbrica e al semaforo imbocca la strada con la staccionata verde…”. Questa descrizione funziona se noi e il nostro amico parliamo dello stesso supermercato e della stessa fabbrica, altrimenti rischiamo di non incontrarci.
Ritroviamo una situazione simile nella descrizione solo a parole di una figura geometrica: la nostra descrizione risulta efficace se il linguaggio e i concetti che utilizziamo sono condivisi con chi ascolta; possiamo verificarlo in modo molto semplice, chiedendo a chi ascolta di replicare il disegno da noi descritto.
Possiamo proporre questo meccanismo in una semplice e divertente attività di geometria: rappresentiamo alcuni concetti geometrici in un disegno – per esempio uno come quello in figura – e chiediamo a un primo studente di spiegare il disegno a un secondo che dovrà disegnarlo; il risultato sarà la conseguenza della comprensione dei concetti da parte di entrambi, della condivisione del linguaggio utilizzato e del loro affiatamento. Se preferiamo possiamo proporre questa attività non a studenti singoli, ma a due gruppi: uno che descrive e l’altro che interpreta e disegna.
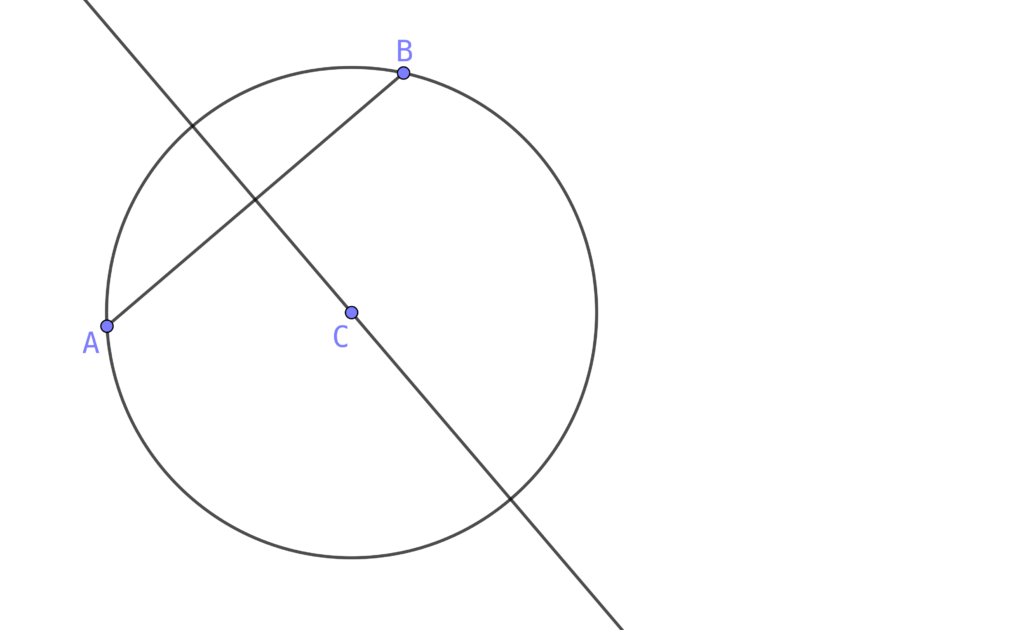
Perché funzioni è opportuno che chi descrive e chi disegna possano comunicare senza essere nella stessa stanza. Anni fa proponevo questa attività chiedendo a un gruppo di ragazzi di uscire con i walkie talkie; in questo periodo, nostro malgrado, la didattica a distanza può esserci d’aiuto. Per esempio abbiamo la possibilità di inviare via mail il disegno da far descrivere al primo gruppo e ricevere sempre via mail il disegno prodotto dal secondo gruppo che ha seguito la descrizione a parole. La comunicazione può consistere in un messaggio vocale registrato, un testo scritto o più semplicemente in un incontro via Zoom o Meet. Il confronto fra i disegni permetterà all’insegnante di stabilire un punteggio dal quale, come in ogni gioco che si rispetti, dipenderà un piccolo premio sia per chi descrive sia per chi disegna: in questo gioco cooperativo, entrambi devono mettere in atto conoscenze e competenze per ottenere un buon risultato. Se nel frattempo torneremo a scuola, potremo sempre chiedere ai ragazzi se hanno voglia e disponibilità di portare dei walkie talkie per un’attività di geometria: ne saranno entusiasti!
