Una delle sfide più importanti per noi insegnanti di matematica è riuscire a trasmettere ai nostri studenti l’idea che la nostra materia possa essere utile per comprendere il mondo che ci circonda e per risolvere in modo razionale molti problemi che incontriamo ogni giorno.
Oggi voglio proporvi un esempio di attività sugli angoli alla circonferenza che si può svolgere in classe per cercare di rafforzare questa idea.
Immaginiamo di trovarci in Piazza della Signoria a Firenze. Attorno a noi possiamo ammirare bellezze architettoniche e scultoree di tutti i tipi, la più famosa sicuramente è la replica del David di Michelangelo.
La celebre statua poggia su un alto piedistallo in modo da poterla ammirare in tutta la sua imponenza.
Se si guarda la statua da lontano la si vedrà piccola perché l’angolo formato dagli estremi della statua e dal nostro occhio sarà piccolo.
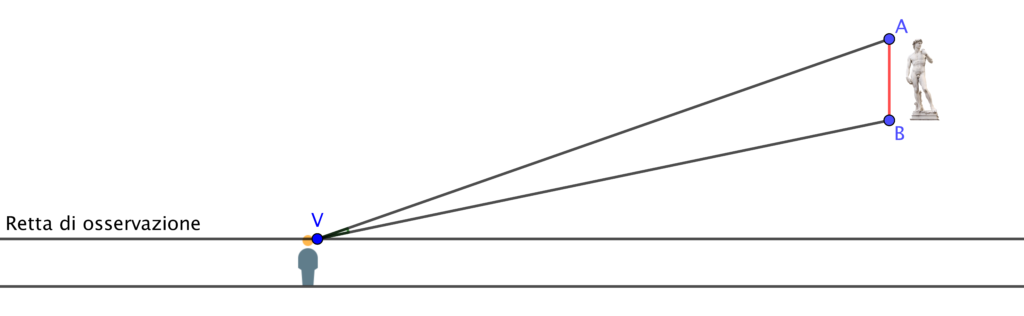
Ma anche se si è troppo vicini al piedistallo la statua formerà un piccolo angolo di visuale e apparirà schiacciata.
Intuitivamente deve esistere una distanza intermedia che rende massimo l’angolo di visuale della statua. Ma come trovare questa distanza ideale?
Si tratta di un antico problema matematico conosciuto come il problema di Regiomontano dal nome (italianizzato) del matematico e astronomo tedesco che lo propose nel 1400.
Il dilemma si risolve in modo elegante con un ragionamento legato agli angoli alla circonferenza.
Prendiamo in considerazione la retta parallela al suolo che passa per i nostri occhi. Questa retta rappresenta le possibili posizioni del punto di osservazione V.
Chiamiamo A e B i due estremi della scultura e immaginiamo di spostare il punto di osservazione V a una distanza tale che la circonferenza che passa per i punti A, B e V sia tangente alla retta di osservazione.
Gli angoli alla circonferenza che insistono sullo stesso arco sono tutti congruenti, per cui se immaginassimo di spostarci lungo i punti della circonferenza vedremmo la statua sempre con le stesse dimensioni apparenti.
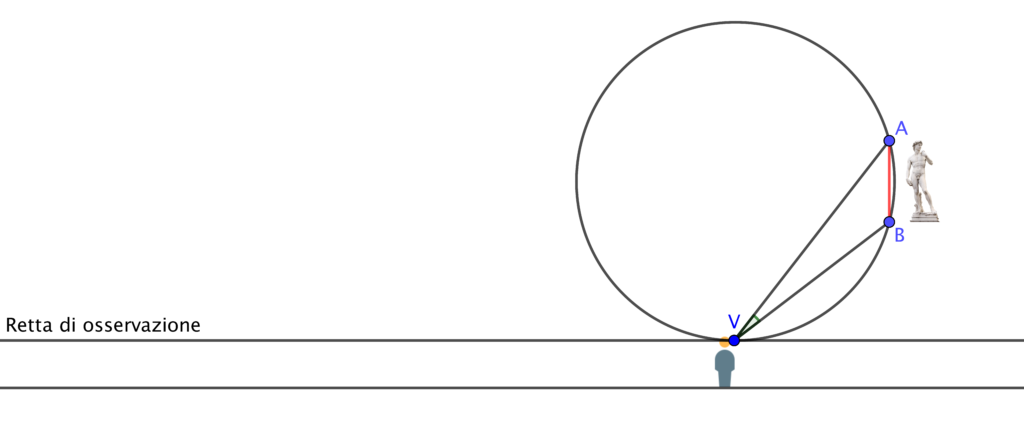
Il punto di tangenza tra la retta e la circonferenza è il punto che rende massimo l’angolo di osservazione.
La dimostrazione è abbastanza semplice. Immaginiamo di prendere un altro punto di osservazione più lontano dalla statua, per esempio il punto C, e chiamiamo D il punto di intersezione tra la circonferenza e il segmento che congiunge C ad A.
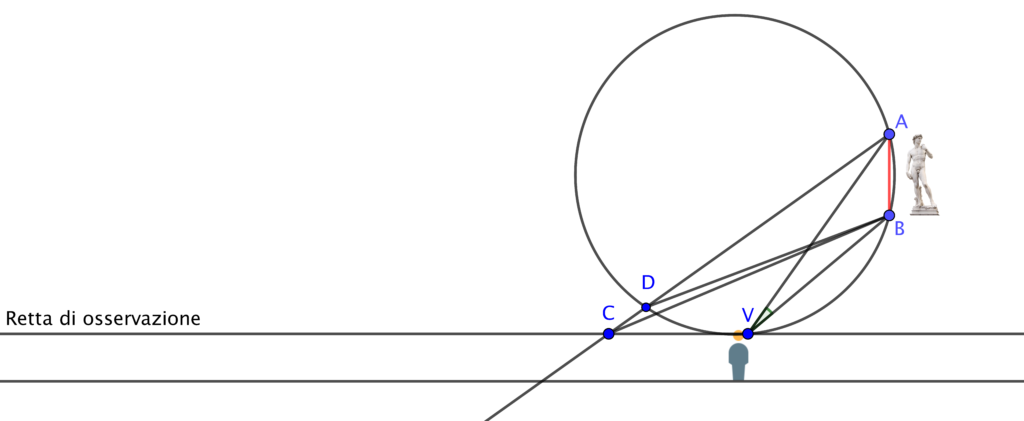
Per considerazioni geometriche di base, l’angolo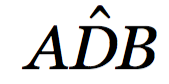 
è maggiore dell’angolo
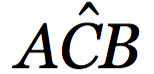
Tuttavia, l’angolo
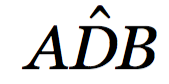
è congruente all’angolo
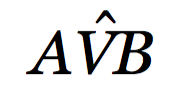
perché sono angoli alla circonferenza che insistono sullo stesso arco.
Di conseguenza, l’ampiezza dell’angolo di visuale in C è minore dell’ampiezza dell’angolo di visuale in V.
Un ragionamento analogo si può fare se il punto di osservazione è più vicino alla statua rispetto al punto di tangenza per cui il punto V rappresenta l’angolo di osservazione massimo.
Questo risultato ha una certa utilità anche nel gioco del rugby!
Quando una squadra segna una meta ha la possibilità di tirare un calcio piazzato per ottenere ulteriori punti. Il giocatore che esegue il tiro può sistemare il pallone in qualsiasi punto del campo che si trovi sulla retta perpendicolare alla linea di fondo tracciata a partire dal punto in cui è stata realizzata la meta.
Per rendere il tiro più facile da eseguire il giocatore deve scegliere una posizione che massimizza l’angolo formato dai pali e la palla.
Il problema può essere presentato in classe in modo efficace usando GeoGebra e, nel caso di studenti che hanno già studiato le derivate, si può aggiungere come attività il calcolo del punto ottimale con metodi di analisi matematica.