
Da alcuni anni cerco di rendere la matematica più tangibile agli studenti (dagli alunni di scuola primaria a quelli universitari) ricorrendo all’antica arte della piegatura della carta: l’origami. Questa scelta è motivata da vari fattori. Prima di tutto le pieghe origami sono state assiomatizzate: alcune di essi sono confrontabili con le costruzioni con riga e compasso di Euclide ma una, in particolare, rende questo sistema assiomatico più ricco di quello con riga e compasso, permettendo anche la soluzione di problemi classici come la trisezione dell’angolo e la duplicazione del cubo. Inoltre, negli ultimi anni, importanti università e centri di ricerca stanno rifacendosi a quest’arte per le sue potenzialità nelle applicazioni tecnologiche.
Quindi l’utilizzo dell’origami in classe permette un approccio diverso, più concreto e motivato alla matematica, correttamente formalizzato.
L’esperienza che vi propongo parte dalla piegatura di un semplice modello origami creato da Paolo Bascetta, insegnante di Liceo scientifico ed esperto di origami: una squadretta con angoli di 45° e 90°. La piegatura supporterà in modo tangibile le risposte a domande su operazioni e oggetti geometrici, che faremo a ogni passaggio, e darà modo anche di discutere matematicamente la possibile generalizzazione del modello. L’attività principale è pensata per ragazzi dagli 11 ai 15 anni, ma darò alcuni spunti anche per i più grandi.
Per piegare il modello si parte da un foglio A4* (o da suoi multipli o sottomultipli).
Partiamo dalle istruzioni di piegatura, illustrate nei disegni detti “diagrammi di piegatura”, cui seguiranno alcune domande matematiche a esse collegate.
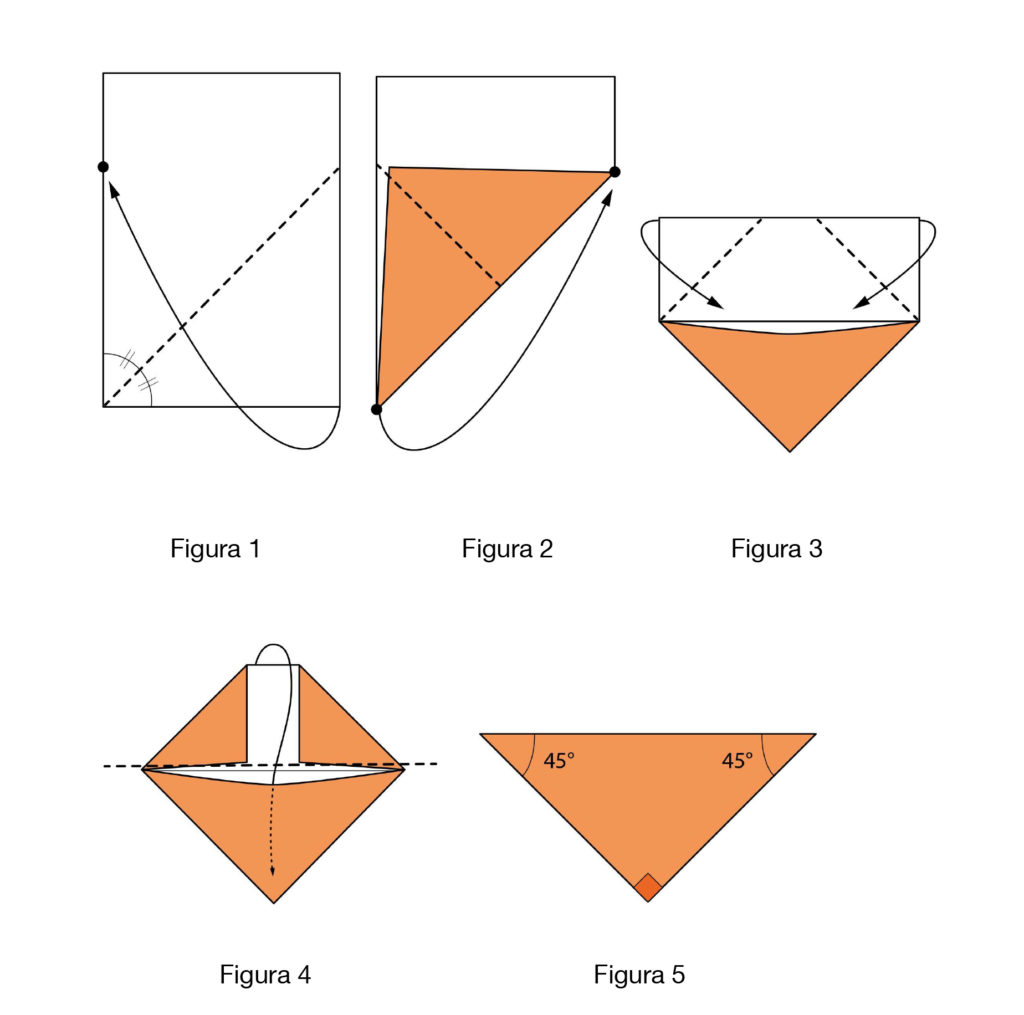
Ne approfitto per dare alcune indicazioni sulla lettura dei diagrammi. Ogni immagine contiene l’istruzione della piega da eseguire il cui risultato compare nella figura successiva. In questo modello le pieghe da eseguire, indicate da linee tratteggiate, sono tutte a valle: una volta piegate e riaperte ricorderanno la valle scavata da un fiume. Le frecce a tratto continuo (figure 1, 2 e 3) mostrano il movimento da eseguire; la freccia tratteggiata della figura 4 indica che la parte di carta piegata va intascata.
Ecco le istruzioni; per fare piegare i ragazzi potete scegliere se utilizzare i termini matematici proposti o farli piegare per imitazione, discutendo in seguito la descrizione matematica:
- piegare la bisettrice dell’angolo retto in basso a sinistra (basta portare il lato corto in basso su quello verticale a sinistra)
- piegare l’altezza del triangolo (rettangolo) colorato (basta portare il vertice in basso a sinistra dell’ipotenusa sull’altro suo vertice)
- portare i lati corti del rettangolo bianco sull’ipotenusa del triangolo colorato
- piegare lungo l’ipotenusa, intascando il trapezio bicolore nel triangolo grande colorato.
Ecco pronta la squadretta!
Le domande da porre durante la piegatura possono essere calibrate secondo la personalità della classe e del programma svolto. Per questo modello proporrò alcune domande:
- Quali poligoni riconosci dopo aver piegato?
Per esempio, nella figura 4 compaiono: un pentagono, tre triangoli rettangoli isosceli, un rettangolo, due trapezi rettangoli, un trapezio isoscele e alcuni poligoni concavi.
- Descrivi il significato geometrico delle pieghe fatte.
Per esempio, nella figura 1, la piega rappresenta la bisettrice dell’angolo retto; nella figura 2, la piega rappresenta l’altezza del triangolo.
- Giustifica perché i triangoli ottenuti nelle figure 2, 3 e 4 sono rettangoli isosceli.
- Descrivi le simmetrie dei modelli ottenuti dopo ogni passaggio.
- Supponendo che le misure del rettangolo di partenza siano a e b con a < b, trova le aree dei poligoni che hai riconosciuto in funzione di a e b.
Si può anche proporre un problem solving: supponendo di partire da un rettangolo qualsiasi di misure a e b con a < b, trova le limitazioni per b perché si possa riproporre la stessa modalità di costruzione della squadretta.
Si ringrazia Nicola Spreafico per la realizzazione dei disegni.
*Forse non tutti sanno che…
Tutti noi siamo abituati a utilizzare fogli A3 e A4; ma qual è la proprietà di questi formati?
L’idea è stata quella di produrre rettangoli A(n), n numero naturale, che divisi lungo l’asse di simmetria parallelo al lato corto diano un rettangolo A(n+1) simile ad A(n).
Se A(n) ha misure a(n) e b(n) con a(n) < b(n), allora
a(n+1) = b(n)/2 e b(n+1) = a(n)
Per la similitudine dei rettangoli, si deve avere
a(n) : b(n) = a(n+1) : b(n+1)
ossia
a(n) : b(n) = b(n)/2 : a(n)
e questo ci dice che b(n) = a(n)√2.
Inoltre, A0 ha lati di lunghezza a(0)= 841 mm e b(0)= 1189 mm, scelti in modo che l’area del foglio A0 sia circa un metro quadrato.
Con facili calcoli, a(4) = a(0)/4 = 210 mm e b(4) = b(0)/4 = 297 mm, con misure arrotondate al millimetro.
Per le scuole superiori questi fogli possono essere presi come spunto per esercizi sulle progressioni (sia rispetto ai loro lati, sia rispetto alle aree).
Leggi l’articolo: Origami, matematica e geometria: una nuova didattica
Leggi l’articolo: (S)piegando… il teorema di duplicazione del seno con gli origami
