Il pensiero computazionale rappresenta un atteggiamento e un insieme di competenze universalmente applicabili che lo rendono fondamentale nel XXI secolo ben oltre la semplice programmazione informatica.
Questo tipo di pensiero, che completa e combina il pensiero matematico, scientifico e ingegneristico, utilizza astrazione e decomposizione nell’affrontare un compito complesso che sia risolvere o porre un problema o progettare un sistema non banale.
Il pensiero computazionale, inoltre, è fondamentale anche per un utilizzo costruttivo dell’Intelligenza Artificiale. L’utilizzo di chat bot è ormai molto diffuso tra studentesse e studenti e noi docenti dovremmo aiutare le nostre alunne e i nostri alunni a non utilizzarli come stampelle digitali, modalità che inficia negativamente sulla capacità di apprendimento. Possedere un adeguato pensiero computazionale aiuta un’interazione umanamente intelligente con i chat bot.
In questo articolo vi propongo un’attività didattica che combina pensiero computazionale e problem solving pratico utilizzando il metodo scientifico. Si tratta di un approccio concreto e tangibile per sviluppare inizialmente abilità di decomposizione (scomporre un problema complesso in parti più semplici), riconoscimento di pattern (identificare regolarità e relazioni causa-effetto), astrazione (focalizzarsi sugli elementi essenziali ignorando i dettagli irrilevanti), costruzione di algoritmi (come procedure sistematiche per la risoluzione di problemi) e soprattutto come contesto di fondo per applicazioni pratiche matematiche, attraverso il troubleshooting di un oggetto di uso quotidiano: la torcia elettrica.
L’attività è flessibile e offre vari livelli di complessità, modulando i quali si può rendere adatta sia alla secondaria di primo grado che di secondo.
Disponendo di più tipi di torce (reali o virtuali), con il gruppo classe si effettua un brainstorming sulle caratteristiche di questi oggetti. Consiglio di porre l’enfasi su questa prima parte di analisi per selezionare le caratteristiche che determinano il funzionamento della torcia.
Il processo di astrazione è uno dei pilastri del pensiero computazionale e della modellizzazione matematica. In questo caso pratico, l’astrazione nella diagnostica della torcia si concretizza nelle seguenti modalità di approccio.
Quando le studentesse e gli studenti analizzano la torcia, devono ignorare dettagli irrilevanti come:
- il colore della torcia
- il materiale dell’involucro (plastica, metallo)
- il peso o le dimensioni
- il marchio del produttore
- la forma estetica
e focalizzarsi sugli elementi essenziali per il funzionamento:
- presenza di energia (pile)
- conversione di energia in luce (lampadina)
- controllo del circuito (interruttore)
- continuità elettrica (collegamenti)
Dato che l’algoritmo diagnostico esaustivo è abbastanza complesso è bene consigliare alla classe di accorpare le ultime due caratteristiche essenziali del funzionamento della torcia in un’unica caratteristica denominata collegamento pile-lampadina.
Suggerisco di introdurre l’esperienza attraverso lo storytelling:
L’altra notte tornando a casa mi sono accorta che mancava l’elettricità e avevo anche lo smartphone scarico! Mi sono però ricordata che mia madre lascia sempre una torcia accanto all’interruttore generale di corrente. Che delusione, provando ad accenderla: non funzionava! Dopo aver inciampato e sbattuto su mobili vari, sono riuscita comunque ad andare in bagno e infine a letto. Il mattino dopo mi sono svegliata con la curiosità di capire perché quell’inutile torcia non funzionava. Pensavo fosse una cosa semplice, invece mi sono persa in vari tentativi fallimentari. Voi avete idea di come fare per individuare esattamente la causa?
Come primo passo studentesse e studenti effettueranno un brainstorming dei possibili problemi:
- pile scariche o mal posizionate
- lampadina bruciata
- collegamento pile-lampadina (interruttore difettoso – circuito interrotto)
Poi saranno invitati (singolarmente o in gruppo) a descrivere un algoritmo che individui esattamente la causa del malfunzionamento, qualsiasi essa sia.
È importante capire la differenza fra ripristinare il guasto rendendo la torcia funzionante ed effettuare una diagnosi esatta della causa del malfunzionamento: è in questa differenza che sta la potenzialità principale di questa esperienza. La maggior parte delle classi commette un errore logico fondamentale che consiste proprio nella non adeguata applicazione del metodo scientifico. Le studentesse e gli studenti iniziano chiedendosi se le pile siano scariche o difettose, quindi sostituiscono le pile e testano la funzionalità della torcia: se si accende possono asserire che il problema era nelle pile. Ma se la torcia non funziona dopo aver cambiato le pile, passano direttamente a esaminare la lampadina. Se la torcia funziona concludono che il problema era la lampadina. Qui l’errore è logico: non ripristinando le pile originali non possono di fatto asserire che il problema era solo nella lampadina e che invece non fossero sia le pile scariche che la lampadina fulminata a causare il malfunzionamento. Di fatto è quasi come se sostituissi due componenti contemporaneamente, non posso distinguere quale fosse effettivamente difettoso. Questo è un concetto fondamentale nel debugging: testare una variabile alla volta.
Di seguito è rappresentato un tipico diagramma di flusso, errato, prodotto inizialmente dalla classe:
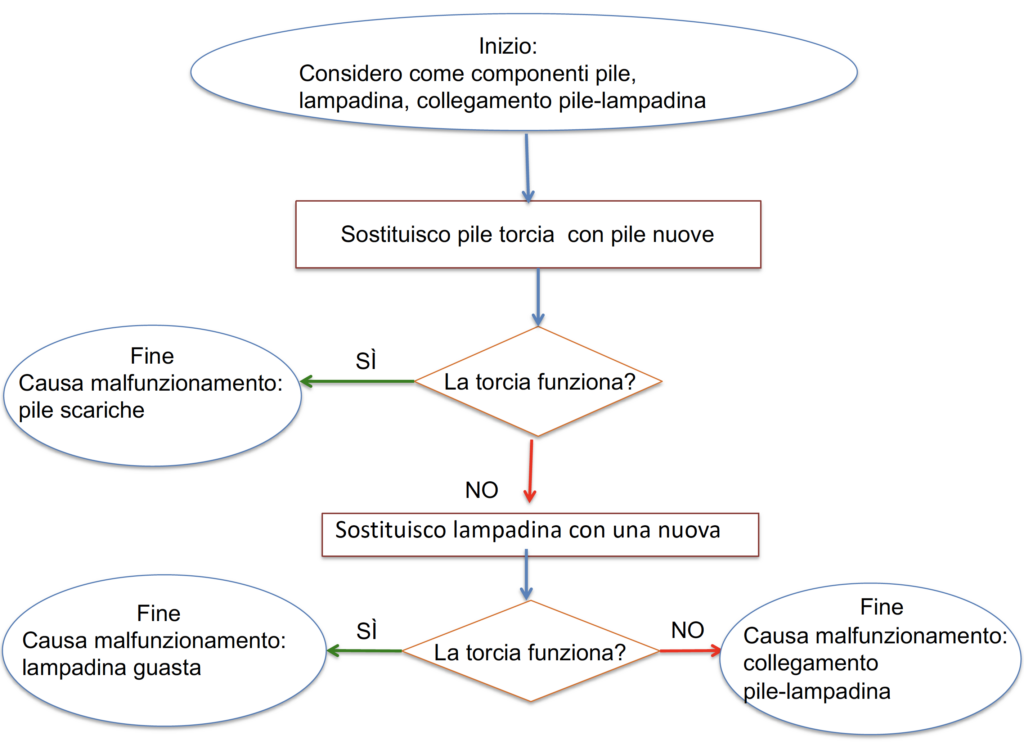
Quindi si invitano studentesse e studenti a testare una variabile per volta, ripristinando dopo ogni passo la situazione iniziale: capiranno da soli che nel caso sfortunato siano più componenti assieme inadeguate, occorre dopo aver testato un elemento per volta testare tutte le combinazioni possibili a due a due fino (nel nostro caso) all’ultima eventuale di tutt’e tre le componenti guaste.
Questo primo diagramma deve essere dunque corretto inserendo prima dell’istruzione di sostituire la lampadina, l’azione di ripristinare le vecchie pile. Così come dopo che si è verificato che sostituendo la lampadina la torcia non funziona, occorre rimettere la vecchia lampadina e controllare il collegamento lampadina-pile, eventualmente ripristinarlo e poi riprovare a vedere se la torcia funziona. In caso affermativo si stabilisce che la causa era nel collegamento pile-lampadina, altrimenti la causa non è dovuta a un singolo componente ma almeno a una coppia e quindi si prosegue agendo su due elementi assieme per tutte le possibili combinazioni.
Questa attività laboratoriale costituisce inoltre l’occasione per rappresentare graficamente la logica di fasi progettuali mediante diagrammi di flusso (comprendente anche scelte condizionate e cicli iterativi) e per ricostruire un processo a partire dalla lettura di un diagramma di flusso elaborato da altri compagne e compagni di classe; quindi rappresenta anche un ulteriore stimolo allo sviluppo delle capacità logico-razionali.
Questa attività ha anche delle applicazioni matematiche. Una prima consiste nel calcolare il numero delle possibili cause:
numero cause $=$ numero dei singoli componenti $+$ numero possibili combinazioni di $3$ elementi a coppie di $2$ $+1$ combinazione (tutti e tre elementi difettosi)
Calcolo combinatorio: $C_{3,2}=\begin{pmatrix}
3 \\
2
\end{pmatrix}=\dfrac{3!}{2!\left( 3-2\right) !}$
numero cause $=3+3+1=7$
Per le classi di primo grado o del primo biennio del secondo grado, si può chiedere di costruire una tabella relativa alle possibili cause e dedurne il numero totale dalla tabella dei risultati possibili:
| Pile OK | Lampadina OK | Collegamento OK | Diagnosi Finale |
| ✗ | ✓ | ✓ | Solo pile difettose |
| ✓ | ✗ | ✓ | Solo lampadina difettosa |
| ✓ | ✓ | ✗ | Solo collegamento difettoso |
| ✗ | ✗ | ✓ | Pile + Lampadina difettose |
| ✗ | ✓ | ✗ | Pile + Collegamento difettoso |
| ✓ | ✗ | ✗ | Lampadina + Collegamento difettoso |
| ✗ | ✗ | ✗ | Tutti e tre i componenti difettosi! |
Questa tabella può essere lo spunto per esercizi di algebra booleana se si aggiunge lo stato:
| Pile OK | Lampadina OK | Collegamento OK | Diagnosi Finale |
| ✓ | ✓ | ✓ | Torcia funzionante |
Si possono proporre poi problemi riguardanti situazioni specifiche per il calcolo delle probabilità, analizzando il concetto di indipendenza statistica, modulandone la complessità a seconda del livello scolastico. Un primo semplice esempio è il seguente.
Se il $20\%$ delle torce ha pile scariche e il $15\%$ lampadine rotte, qual è la probabilità di avere entrambi i problemi?
Si può aumentare la complessità del caso di studio separando i componenti interruttore e circuito, passando quindi da tre a quattro e chiedere alle studentesse e agli studenti come cambia il numero dei casi possibili (numero di possibili cause di malfunzionamento). Per esempio si potrebbero proporre problemi semplici ma più articolati, come il seguente.
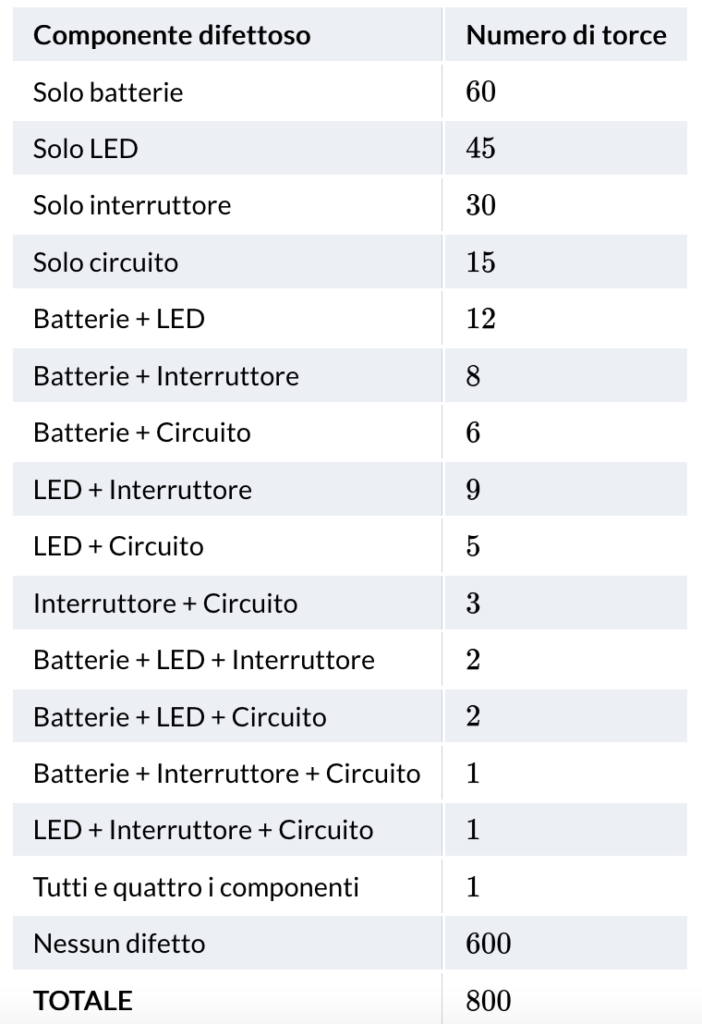
Un’azienda italiana produce torce LED per escursionismo. Il reparto controllo qualità testa un campione di $800$ torce prima della spedizione e registra i difetti riscontrati.
Domande possibili dirette:
1) Quante torce del campione sono perfettamente funzionanti?
2) Quante torce presentano almeno un difetto?
3) Qual è la probabilità che una torcia scelta a caso dal campione sia perfettamente funzionante?
• Esprimi il risultato come frazione ridotta ai minimi termini
• Esprimi il risultato come numero decimale
• Esprimi il risultato come percentuale
4) Se l’azienda spedisce un lotto di $2400$ torce, quante torce difettose ci aspettiamo di trovare nel lotto?
Ulteriori domande per casi specifici:
1) L’azienda spedisce una confezione con $3$ torce scelte a caso dal lotto. Qual è la probabilità che:
• Tutte e tre siano funzionanti?
• Almeno una sia difettosa?
• Esattamente una sia difettosa?
2) Un cliente acquista $5$ torce. Qual è la probabilità che tutte siano perfette?
Per gli ultimi anni della scuola secondaria di secondo grado si può aggiungere:
Garanzia di qualità
L’azienda vuole garantire che in una confezione da $10$ torce ci sia almeno una probabilità del $95\%$ che tutte funzionino. Qual è la probabilità massima di difetto singolo accettabile per raggiungere questo obiettivo?
Si potrebbero anche fornire tabelle di costi per minuto di lavoro (diversi fra loro) e di sostituzione/riparazione di ciascun componente e chiedere di predisporre una strategia che ottimizzi i costi di diagnostica; oppure si potrebbero fornire probabilità diverse di guasto per ciascun componente ($p_{1}$, $p_{2}$,, $p_{3}$, $p_{4}$) e misurare l’incertezza della variabile discreta $X$ con valori ($x_{1}$, $x_{2}$,, $x_{3}$, $x_{4}$) che rappresenta lo stato della torcia.
Queste vogliono solo essere alcune delle molteplici applicazioni matematiche di questa iniziale attività laboratoriale, ma vi invito a cercare sempre di sfruttare le ulteriori molteplici potenzialità di un’attività laboratoriale, a seconda della vostra creatività ed esigenza del momento.