Il Biancomangiare è un dolce così chiamato perché gli ingredienti usati per realizzarlo sono tutti di colore bianco. Da esso trae spunto il nome di una celebre curva, chiamata, appunto, in inglese, Blancmange curve, detta anche curva di Takagi, che è stata proposta nel 1903 dal matematico giapponese Teiji Takagi. Anche se potremmo annoverare l’argomento tra le “curiosità” matematiche, penso che abbia un interesse didattico, come esempio di grafico di una funzione continua in tutto il suo dominio ma non derivabile in alcun punto.
Si tratta di una curva frattale, di cui è possibile costruire un’approssimazione utilizzando GeoGebra: qui di seguito un esempio di scheda didattica da utilizzare in classe.
Conviene impostare la griglia di GeoGebra in modo che ogni quadratino abbia lato $0,5$.
1. Disegna il grafico della funzione predefinita round$\left(x\right)$ e denominala con $a\left(x\right)$. Che tipo di grafico hai ottenuto? Come opera questa funzione?
2. Disegna il grafico della funzione $b\left(x\right)=x-a\left(x\right)$. Che tipo di grafico hai ottenuto?
3. Disegna il grafico della funzione $s\left(x\right)=\left|b\left(x\right)\right|$, mediante il comando s(x) = abs(b(x)). Che cosa rappresenta questa funzione?
La curva di Takagi è il grafico della funzione che ha la seguente espressione:
$f\left( x\right) =\sum ^{+\infty }_{k=0}\dfrac{s\left( 2^{k}x\right) }{2^{k}}$
Si tratta quindi di una somma infinita di funzioni del tipo disegnato al punto 3.
Noi ci limiteremo a tracciare le sue approssimazioni per $k$ che varia da $0$ a $10$.
4. Crea uno slider $k$, variabile da $0$ a $10$, con incremento uguale a $1$, e portalo al valore $0$.
5. Disegna i grafici delle funzioni che sono i termini della successione associata alla serie:
$u_{k}\left( x\right) =\dfrac{s\left( 2^{k}x\right) }{2^{k}}$
Che tipo di funzione visualizzi per $k=0$?
Fai aumentare $k$ e osserva il grafico che ottieni. Come cambia? Spiega perché il grafico cambia in questo modo.
Ora che hai visualizzato le onde triangolari, occorre disegnare il grafico che si ottiene dalla loro somma. Riporta $k$ a $0$.
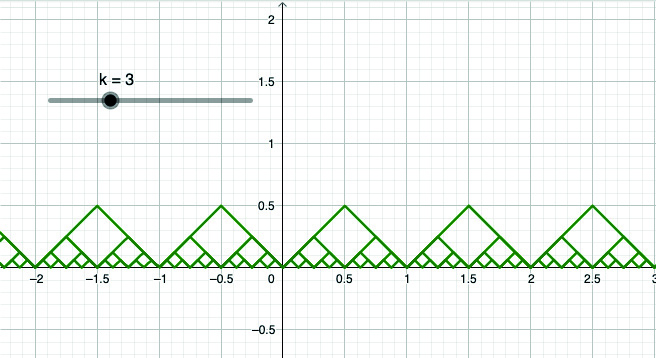
6. Inserisci il comando Successione(s(2^i x) / 2^i, i, 0, k): esso ti permette di disegnare la successione delle funzioni corrispondenti a un certo valore di $k$. Per $k=0$ visualizzi la funzione $u_{0}$, per $k=1$ visualizzi $u_{0}$ e $u_{1}$ e così via (figura 1). Verificalo.
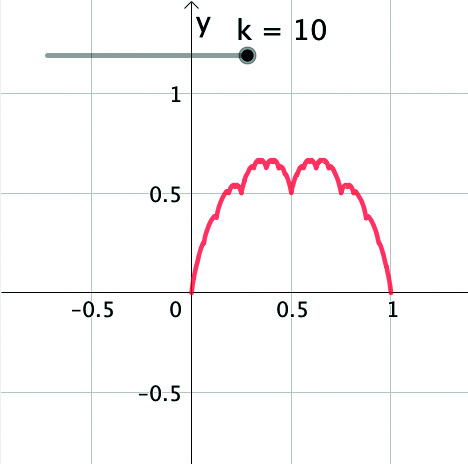
7. Il comando precedente ha creato una lista di funzioni e l’ha denominata automaticamente l1. Per disegnare il grafico della funzione somma puoi digitare il comando c(x) = Somma(l1, k). Indica infine con $f\left( x\right)$ la funzione che si ottiene restringendo $c\left( x\right) $ all’intervallo $\left[ 0;1\right] $. In figura 2 è mostrato il grafico che si ottiene per $k=10$.
8. Riporta $k$ a $0$, disegna la funzione $f’\left(x\right)$ e osserva il suo comportamento all’aumentare di $k$. Che cosa puoi dire? Che cosa puoi ipotizzare che succeda al grafico di $f’\left(x\right)$ quando $k\rightarrow +\infty $?
Abbiamo messo in evidenza il fatto che, all’aumentare di $k$, le funzioni che approssimano $f\left( x\right)$ sono tutte continue ma hanno un numero di punti in cui non sono derivabili che aumenta sempre di più.
La funzione $f\left( x\right)$ risulta quindi continua ovunque, ma non derivabile, perché ha infiniti punti in cui non lo è.
Questo è un esempio del fatto che la continuità non implica la derivabilità.
Questa attività di esplorazione è tratta da “Matematica allo specchio edizione Blu – II biennio e V anno”, il nuovo corso di Matematica edito da Ghisetti e Corvi.