
Negli ultimi anni la pandemia da Covid-$19$ ha sollevato numerose questioni, tra le quali la necessità di migliorare i sistemi di aerazione di scuole, uffici e ambienti di lavoro. La qualità dell’aria che respiriamo è in effetti un elemento cruciale per prevenire numerose patologie, non soltanto di origine virale, a carico dell’apparato respiratorio. Tra queste è particolarmente importante il tumore ai polmoni, per il quale il maggiore fattore di rischio nei soggetti non fumatori è rappresentato da un nemico sconosciuto e subdolo: il radon.
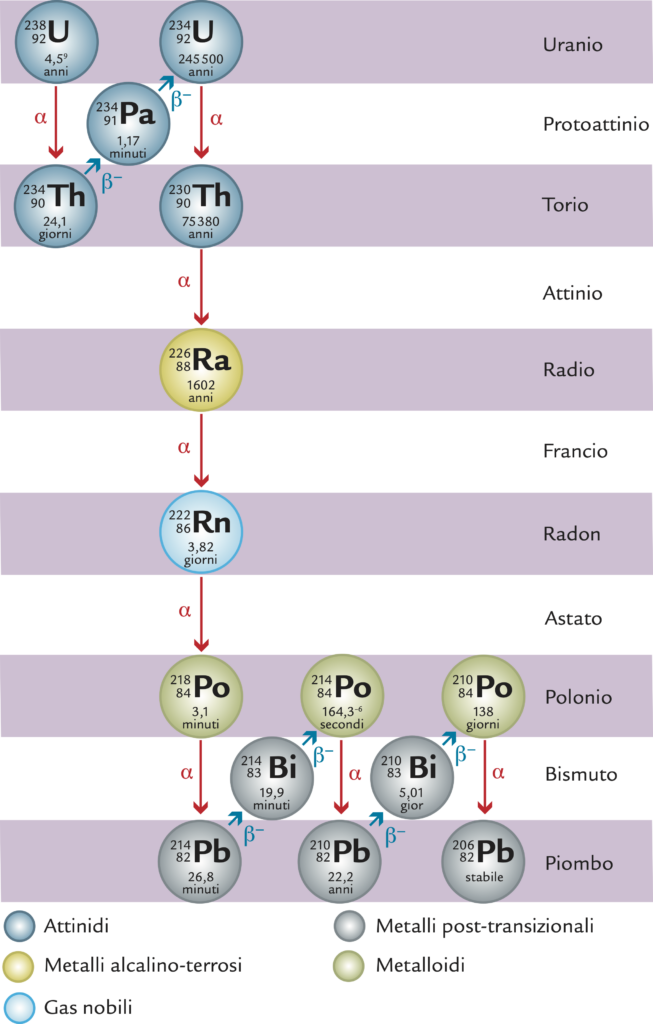
Il radon è un gas chimicamente inerte, inodore e incolore, presente in natura per il $99\% $ mediante l’isotopo $^{222}$Rn, prodotto dal decadimento radioattivo dell’isotopo $226$ del radio1 ($^{226}$Ra) e a sua volta instabile per emissione di una particella alfa (nucleo di $^{4}$He). Il radio è il risultato di una sequenza di decadimenti radioattivi che hanno come progenitore l’isotopo $238$ dell’uranio ($^{238}$U), presente nelle rocce della crosta terrestre in concentrazioni variabili da una parte per milione a qualche percento. Quasi tutti i nuclidi ottenuti dall’uranio-$238$ per decadimenti successivi sono solidi e sono presenti anch’essi nel suolo e nei materiali da costruzione. Il radon costituisce l’unica eccezione perché è in forma gassosa e perciò tende a raggiungere l’atmosfera o, in misura minore, a essere solubilizzato nelle acque sotterranee.
Perché il radon è un pericolo per la salute? Il radon e la sua progenie a breve termine – che possono essere inalati con la respirazione – decadono emettendo particelle alfa, che sono radiazioni ionizzanti. I tessuti biologici in cui essi vengono intrappolati sono dunque sottoposti a una continua cessione di energia, che ha come prodotto primario la produzione di radicali (H e OH). Questi ultimi innescano a loro volta ulteriori processi che portano alla degradazione delle molecole biologiche (anche a livello del DNA) che costituiscono le cellule e i tessuti.
Inoltre il radon è un elemento ubiquitario: si trova all’aperto, in concentrazioni molto basse, ma si accumula negli ambienti chiusi e negli edifici2 (residenziali o di lavoro) nei quali trascorriamo la maggior parte del nostro tempo. Esso dunque rappresenta un pericolo potenziale per tutta la popolazione e una minaccia concreta per alcune categorie di lavoratori.
La correlazione tra esposizione a radon e tumore polmonare è stata riconosciuta dall’Organizzazione Mondiale della Sanità (OMS), che nel $1988$, attraverso l’IARC (International Agency for Research on Cancer), ha classificato il radon (assieme ai suoi prodotti di decadimento) come agente cancerogeno del Gruppo $1$3, cioè come una sostanza avente accertata oncogenicità.
In questo articolo vi propongo un’attività di esplorazione delle funzioni esponenziali, propedeutica all’introduzione del concetto di logaritmo.
L’attività può essere suddivisa in una prima parte incentrata sulle competenze disciplinari e in una seconda parte di sensibilizzazione sugli aspetti sanitari e radioprotezionistici.
Questo schema può essere utile per gli aspetti matematici:
- si introduce il concetto di tempo di dimezzamento, caratteristico di ciascun radioisotopo, e si chiede alle studentesse e agli studenti di completare una tabella come la tabella 1 qui proposta, che riassuma la frazione di isotopi presenti in funzione del tempo;
- si introduce la definizione di progressione aritmetica e di progressione geometrica e, dopo aver stimolato studentesse e studenti a identificarle nella prima e nella seconda colonna della tabella, si chiede di determinare l’espressione analitica che descrive la popolazione di radioisotopi in funzione del tempo;
- attraverso un software come GeoGebra, si chiede a studentesse e studenti di rappresentare la funzione ottenuta e di individuarne le caratteristiche (monotonia, invertibilità);
- a partire dalla funzione esponenziale così ottenuta (di base $\dfrac{1}{2}$) si prova a determinare, in modo approssimato, l’espressione analitica di una funzione esponenziale di base differente e maggiore di $1$. È utile partire dalla base $2$, reciproco di $\dfrac{1}{2}$, in modo da ottenere la funzione richiesta semplicemente cambiando il segno dell’esponente (ricordare le potenze con esponente negativo!). Il passo successivo è scegliere una base che non sia una potenza intera di $\dfrac{1}{2}$ (o di $2$), per esempio $10$. In questo caso è possibile determinare, per approssimazioni successive, un esponente decimale finito $y$ tale che $10^{y}\simeq 2$ (cfr. tabella 2). A questo punto si può introdurre la definizione formale di potenza con esponente reale, con le relative proprietà, e successivamente quella di logaritmo.
Tabella 1 – Popolazione di radionuclidi nel tempo
| Tempo (in unità del tempo di dimezzamento) | $\dfrac{N}{N_{0}}$ | Percentuale residua di radionuclidi |
| $0$ | $1$ | $100\%$ |
| $1$ | $\dfrac{1}{2}$ | $50\%$ |
| $2$ | $\dfrac{1}{4}$ | |
| $12,5\%$ | ||
| $\dfrac{1}{16}$ | ||
| $\dfrac{1}{32}$ | ||
| … | … | … |
| $8$ |
La tabella 1 mostra che, trascorso un intervallo di tempo di circa $6$ volte il tempo di dimezzamento (che nel caso del radon-$222$ è di $3,8$ giorni), la popolazione del radioisotopo è dell’ordine di qualche percento rispetto al valore iniziale.
È lecito chiedersi a questo punto come mai, se dopo qualche settimana la popolazione di radon è praticamente irrilevante, ci si pone il problema dell’esposizione a questo agente oncogeno. La risposta risiede nel fatto che il radon è continuamente formato dal decadimento del suo nuclide “padre”, il radio-$226$, in maniera tale che il numero di decadimenti per unità di tempo del primo eguagli praticamente quelli del secondo. Questa condizione va sotto il nome di equilibrio secolare e fa sì che, in un dato ambiente, il numero di decadimenti di radon per unità di tempo e di volume (detto concentrazione di attività e misurato in Bq/m$^{3}$) si mantenga pressoché costante a parità di condizioni esterne (temperatura, pressione, umidità, flussi d’aria in ingresso e/o in uscita).
Tabella 2 – Risoluzione approssimata dell’equazione $10^{y}=2$
| $y$ | $10^{y}$ |
| $0$ | $1$ |
| $0,5$ | |
| $0,4$ | |
| $0,35$ | |
| $0,33$ | |
| $0,32$ |
La seconda parte può essere affrontata partendo dal numero di tumori polmonari attribuiti al radon. I dati più recenti relativi all’Italia e suddivisi per regione sono riassunti nella seguente tabella4.
Tabella 3 – Tumori polmonari attribuibili al radon (Italia, $2010$) e concentrazione di radon rilevata
| Regione | Casi osservati | Casi stimati | Percentuale di casi osservati | Concentrazione media5 [Bq/m$^{3}$] |
| Abruzzo | $558$ | $49$ | $58$ | |
| Basilicata | $219$ | $10$ | $30$ | |
| Calabria | $665$ | $26$ | $25$ | |
| Campania | $2822$ | $372$ | $95$ | |
| Emilia-Romagna | $2886$ | $190$ | $49$ | |
| Friuli Venezia Giulia | $775$ | $106$ | $162$ | |
| Lazio | $3121$ | $499$ | $121$ | |
| Liguria | $1212$ | $69$ | $38$ | |
| Lombardia | $5718$ | $862$ | $124$ | |
| Marche | $764$ | $34$ | $29$ | |
| Molise | $108$ | $7$ | $43$ | |
| Piemonte | $2816$ | $280$ | $70$ | |
| Puglia | $1706$ | $131$ | $52$ | |
| Sardegna | $746$ | $69$ | $64$ | |
| Sicilia | $2054$ | $109$ | $35$ | |
| Toscana | $2231$ | $159$ | $35$ | |
| Trentino Alto Adige | $401$ | $35$ | $130$ | |
| Umbria | $455$ | $39$ | $58$ | |
| Valle d’Aosta | $69$ | $5$ | $83$ | |
| Veneto | $2808$ | $238$ | $94$ | |
| TOTALE | $32134$ | $3237$ |
Oltre a calcolare la percentuale per ciascuna regione (e a confrontare i dati della propria regione con la media nazionale) è interessante stabilire se esiste una correlazione tra i tumori radon-attribuiti e le concentrazioni6 di radon rilevate. A questo scopo, utilizzando un foglio di calcolo, occorrerà ordinare i dati della tabella secondo la concentrazione crescente di radon e rappresentare in funzione di quest’ultima, in un grafico a dispersione, la percentuale di tumori radon attribuiti.
L’analisi del problema nei suoi molteplici aspetti utilizza strumenti matematici connessi con le competenze acquisite nel corso del secondo biennio e quinto anno, dalle funzioni esponenziali e dalle proprietà dei logaritmi fino ai contenuti di analisi matematica.
In Zona Matematica, nell’area dedicata all’Educazione civica, trovi schede di lavoro per affrontare il problema nei suoi molteplici aspetti
> Vai all’area Educazione civica
1 Il radio è l’elemento la cui scoperta, ad opera dei coniugi Curie, segnò nel $1898$ l’inizio dello studio della radioattività. Tutte le catene radioattive naturali contengono un isotopo del radio che decade in un isotopo del radon.
2 Il radon penetra negli edifici attraverso microfessure del sottosuolo, canalizzazioni di impianti idraulici o di scarico, oppure è presente in molti materiali da costruzione (per esempio tufo, granito, porfido, marmo, argille, gessi e sabbie).
3 List of Classifications – IARC Monographs on the Identification of Carcinogenic Hazards to Humans p. 9
4 Rischio di tumore polmonare attribuibile all’esposizione al radon nelle abitazioni delle regioni italiane – primo rapporto sintetico, 2010 (CCM, ISS) — ARPAT
5 I dati riassunti in tabella sono quelli delle campagne regionali più recenti o della campagna nazionale del $1998$-$2000$ in assenza di ulteriori dati regionali. È possibile reperire i dati ai link Categoria: Quanto radon c’è… e Mappe della concentrazione del radon nelle Regioni italiane.
