
I carburanti rappresentano la fonte energetica che consente di muovere merci e persone; nel mondo interconnesso e globalizzato in cui viviamo non stupisce dunque che un aumento dei loro prezzi abbia ricadute significative su tutti i settori dell’economia. L’impennata cui abbiamo assistito nello scorso anno – in buona parte dovuta al conflitto tra Russia e Ucraina – è diventata centrale nel dibattito pubblico e, in Italia, ha portato all’adozione di una serie di misure1 atte a contenere i prezzi di gasolio e benzina.
Oltre a quello sul bilancio di famiglie e imprese, i carburanti di origine fossile hanno, com’è noto, un pesante impatto ambientale, contribuendo a circa il $30\%$ delle emissioni di CO$_{2}$ e al rilascio di altri inquinanti (particolato, biossido di azoto, monossido di carbonio). Il loro progressivo abbandono è pertanto cruciale ai fini della transizione ecologica. Le politiche di supporto alla mobilità sostenibile, come l’uso di mezzi pubblici o di mezzi privati condivisi, rappresentano dunque una misura concreta di tutela del potere d’acquisto delle famiglie, oltre che di salvaguardia della salute individuale e collettiva e di contrasto al cambiamento climatico.
In questa attività di Educazione civica ci soffermeremo sugli aspetti economici del problema, riservando la trattazione delle implicazioni ambientali al prossimo articolo. In particolare vi propongo un’attività esplorativa che, partendo dalla composizione del prezzo del carburante, conduca studentesse e studenti a passare dai concetti di percentuale ed equazione a quello di funzione. Mostreremo la differenza tra una funzione lineare e una non lineare e faremo alcune considerazioni sulla/e variabile/i indipendente/i. Collateralmente (ma non secondariamente) studentesse e studenti entreranno in contatto con i concetti di accisa e IVA (di cui si può spiegare la differenza) e applicheranno le funzionalità di un foglio di calcolo a un compito di realtà.
Parte A: la composizione del prezzo
Il prezzo dei carburanti che vediamo alle pompe di benzina è il risultato di diverse componenti, il cui peso differisce leggermente da un combustibile all’altro, e che possono essere essenzialmente suddivise in una componente industriale e una fiscale. La prima include il costo della produzione e lavorazione della materia prima ($30\%$ del prezzo finale) e il cosiddetto margine lordo ($12\%$ del prezzo finale per la benzina, $10\%$ per il gasolio), che comprende il guadagno del gestore, i costi di distribuzione primaria e secondaria e una serie di obblighi di legge (tasse locali, portuali, scorte strategiche ecc.). La seconda componente, invece, è costituita dalle imposte (accise e IVA). Possiamo sottoporre alle studentesse e agli studenti il grafico seguente, ottenuto dai dati del MASE (Ministero dell’Ambiente e della Sicurezza Energetica) relativi al terzo trimestre $2023$, dai quali emerge che la componente fiscale prevale su quella industriale.
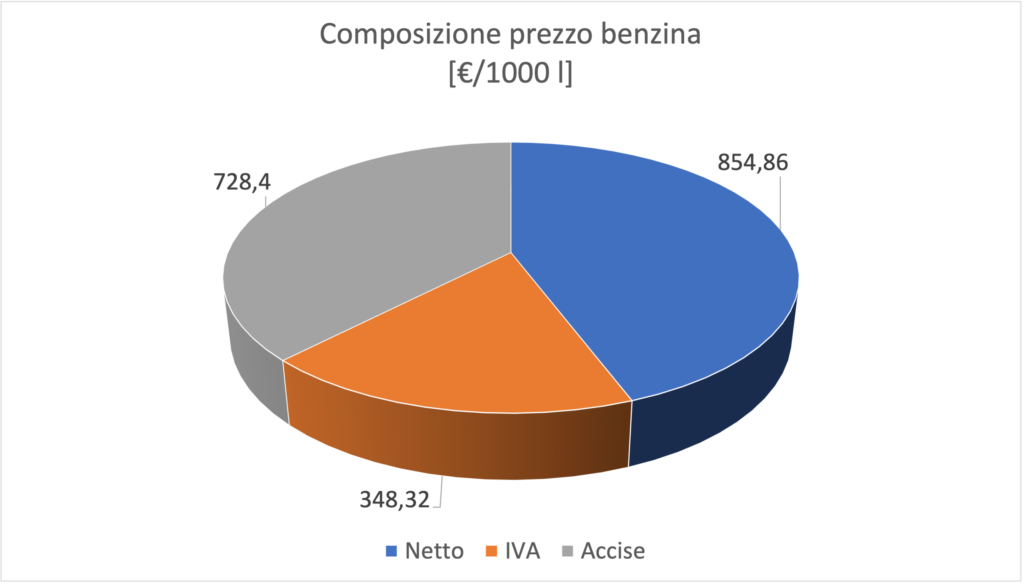
Il grafico si presta a diverse considerazioni:
- Quanto pesa ciascuna voce sul totale?
- L’IVA sui carburanti è al $22\%$. Questo valore è in accordo con il risultato trovato al punto precedente? In che modo possiamo ricavare il prezzo a cui viene applicata l’IVA partendo dal prezzo finale?
Stimoliamo studentesse e studenti a costruire un’equazione del tipo $p_{f}=p_{in}+0,22p_{in}$, in cui $p_{f}$ e $p_{in}$ rappresentano, rispettivamente, il prezzo con e senza IVA. La soluzione $p_{in}=\dfrac{p_{f}}{1,22}$ porta con sé anche un’informazione accessoria: l’IVA si applica anche alle accise, cioè $p_{in}=p_{n}+a$, con $p_{n}$ che indica il prezzo al netto delle imposte e $a$ le accise.
- A questo punto sappiamo che il prezzo finale dipende da tre grandezze (prezzo della materia prima, accise e IVA), tutte variabili nel tempo. Il costo della materia prima è infatti influenzato (al netto di speculazioni) dalla domanda e dall’offerta di petrolio sui mercati mondiali e anche dal cambio dollaro-euro (dato che il petrolio viene pagato in dollari), mentre le accise e l’IVA sono governate da scelte di politica nazionale. Siamo quindi davanti al concetto di funzione e, addirittura, di più variabili: $p_{f}=\left(p_{n}+a\right) \left(1+i\right)$, dove $i$ indica l’IVA.
Possiamo utilizzare GeoGebra o un foglio di calcolo per far disegnare e confrontare a studentesse e studenti le funzioni $p_{f}(p_{n})$ (fissati2 $a=728,4$ e $i=0,22$), $p_{f}(i)$ (fissati $a=728,4$ e $p_{n}=854,86$), $p_{f}(a)$ (fissati $i=0,22$ e $p_{n}=854,86$), ottenute trattando come costanti due variabili per volta tra le tre in esame. In tutti i casi avremo funzioni lineari, ma non di proporzionalità diretta, che studentesse e studenti potranno esplorare per prevedere gli effetti della variazione di una sola componente per volta sul prezzo finale. Potranno inoltre confrontare le loro conclusioni, in particolare relative a un intervento sulle accise, con quanto effettivamente osservato nel $2022$.
È molto importante far comprendere alle studentesse e agli studenti che, sebbene queste voci siano quelle sulle quali è possibile un intervento diretto dello Stato (a differenza del costo della materia prima che è legato alle dinamiche dei mercati internazionali), le accise contribuiscono al gettito erariale e dunque la scelta di una loro riduzione va ponderata in un più ampio quadro di interventi che tengano conto della complessità del bilancio pubblico. Per avere un’idea dei numeri in gioco, può essere utile ricordare che la misura emergenziale adottata dal governo Draghi con il Decreto Legge n. $21$ del $2022$ ha comportato oneri per oltre $4,5$ miliardi di euro per le casse statali, una cifra pari a circa il $10\%$ delle spese annue per l’istruzione.
Possiamo inoltre confrontare il peso delle singole voci di spesa su tre diversi tipi di carburante analizzando la figura 2, dalla quale è abbastanza evidente che la benzina è il carburante su cui la componente fiscale incide maggiormente:
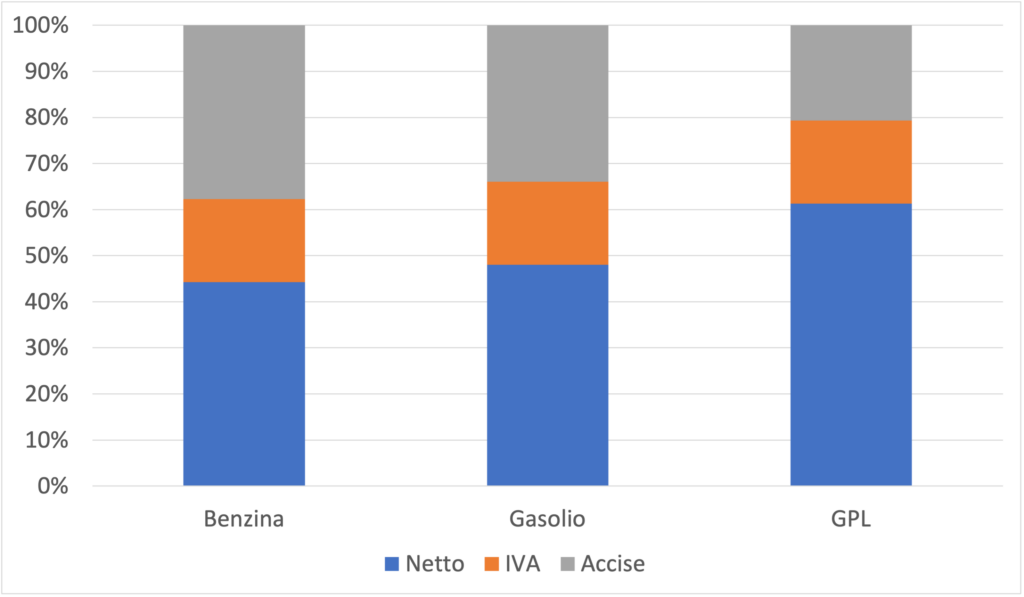
Per contestualizzare i dati italiani a livello europeo, è utile analizzare la seguente tabella, basata sui dati relativi al bollettino settimanale della fine di ottobre (a questo link è possibile accedere all’ultimo bollettino disponibile).
Prezzi di benzina e gasolio in Europa [euro per $1000$ l] – Ottobre $2023$
Paese | Benzina prezzo netto | Benzina prezzo finale | Gasolio prezzo netto | Gasolio prezzo finale |
| Austria | $783,86$ | $1617$ | $967,12$ | $1745$ |
| Belgio | $814,01$ | $1711,15$ | $946,14$ | $1871,02$ |
| Bulgaria | $822,98$ | $1423,2$ | $873,26$ | $1444,27$ |
| Croazia | $794,4$ | $1563$ | $1007,4$ | $1738$ |
| Cipro | $876,25$ | $1565,98$ | $1028,33$ | $1712,45$ |
| Repubblica Ceca | $789,95$ | $1586,24$ | $925,42$ | $1608,28$ |
| Danimarca | $915,13$ | $1938,12$ | $1075,78$ | $1897,93$ |
| Estonia | $905,33$ | $1762$ | $1010,5$ | $1659$ |
| Finlandia | $879,2$ | $1986$ | $1123,35$ | $2026$ |
| Francia | $850,88$ | $1850,61$ | $959,14$ | $1881,77$ |
| Germania | $846,85$ | $1868$ | $990,19$ | $1827$ |
| Grecia | $813,69$ | $1896$ | $1036,96$ | $1812$ |
| Ungheria | $921,96$ | $1583,16$ | $1045,27$ | $1707,69$ |
| Irlanda | $874,99$ | $1846,7$ | $956,91$ | $1849,6$ |
| Italia | $825,27$ | $1895,48$ | $926,62$ | $1883,7$ |
| Lettonia | $846,54$ | $1702,43$ | $960,2$ | $1730,71$ |
| Lituania | $818,68$ | $1554,46$ | $929,62$ | $1574,96$ |
| Lussemburgo | $826,67$ | $1583$ | $983,32$ | $1638$ |
| Malta | $586,21$ | $1340$ | $553,02$ | $1210$ |
| Olanda | $878,93$ | $2028$ | $1038,56$ | $1891$ |
| Polonia | $733,26$ | $1371,37$ | $775,88$ | $1377,17$ |
| Portogallo | $864,15$ | $1774$ | $960,51$ | $1726$ |
| Romania | $830,72$ | $1413,86$ | $960,22$ | $1533,61$ |
| Slovacchia | $794,68$ | $1606$ | $999,85$ | $1677$ |
| Slovenia | $745,01$ | $1548,43$ | $910,57$ | $1674,85$ |
| Spagna | $901,58$ | $1662,87$ | $988$ | $1654,07$ |
| Svezia | $856,06$ | $1743,81$ | $1359,09$ | $2133,75$ |
Possiamo chiedere alle studentesse e agli studenti di:
- determinare il prezzo medio al litro di benzina e gasolio a livello europeo e confrontarlo con quello italiano;
- determinare la deviazione standard per capire quanto i dati siano omogenei tra i Paesi;
- determinare e confrontare il peso della componente fiscale nei vari Paesi;
- stabilire se c’è una politica di tassazione differente tra i due tipi di carburante nei vari Paesi.
Per la benzina il confronto tra i prezzi finali può essere ulteriormente esteso a livello mondiale, utilizzando i dati disponibili a questo link.
Parte B: le fluttuazioni del prezzo
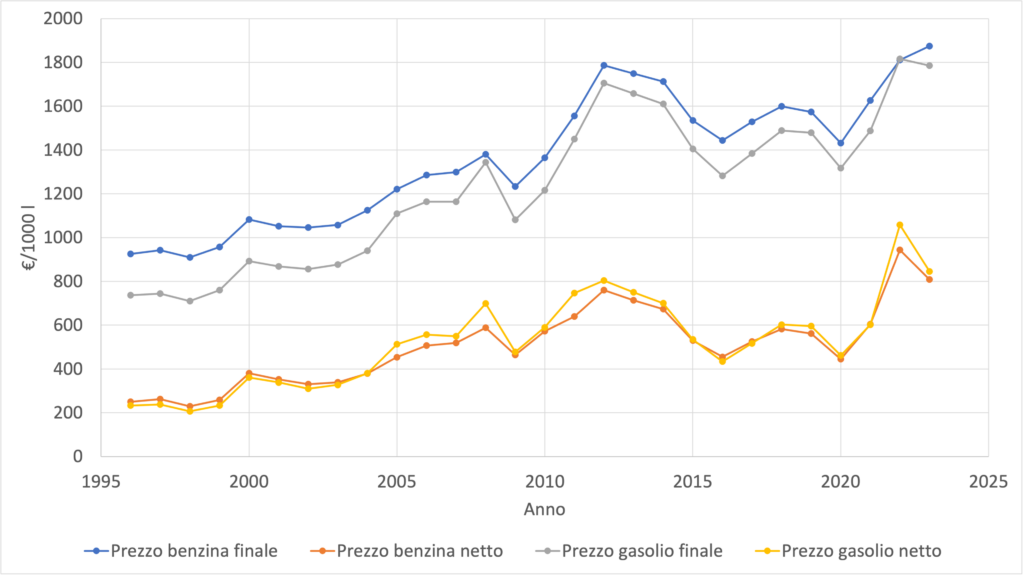
Il passo successivo è analizzare l’andamento del prezzo dei carburanti nel tempo, riassunto nella figura 3, che rappresenta un chiaro esempio di funzione (del tempo) di tipo non lineare. Che tipo di funzione lo descrive? Possiamo invitare le studentesse e gli studenti a riprodurre la curva $p(t)$, relativa al prezzo netto, utilizzando il grafico a dispersione di un foglio di calcolo (per comodità i dati sono disponibili nella tabella in appendice) con l’aggiunta di una linea di tendenza polinomiale. È utile indicare il tempo rispetto al $1996$, assunto come “anno zero”.
La figura 3 evidenzia un generale trend di aumento nel lungo termine, nonostante ampie fluttuazioni, sia per la benzina che per il gasolio; possiamo stimolare un confronto in aula su cosa può aver prodotto le variazioni dal $2019$ a oggi.
Il grafico indica anche che in Italia la componente fiscale è sempre stata più alta per la benzina che per il gasolio (i prezzi finali differiscono apprezzabilmente, a differenza di quelli netti) e possiamo proporre alle studentesse e agli studenti di confermare graficamente tale conclusione accedendo direttamente ai dati del MASE per costruire, tramite un foglio di calcolo, l’andamento nel tempo della componente fiscale.
Qual è la scala temporale su cui varia davvero il prezzo dei carburanti? I dati della figura 3 illustrano il prezzo annuale medio, ma in realtà esiste una forte stagionalità: nel nostro Paese (e in tutto l’emisfero settentrionale) il gasolio ha costi più alti nei mesi autunnali e invernali, poiché c’è domanda di gasolio (e dei suoi derivati) anche per il riscaldamento. Il prezzo della benzina, invece, cresce solitamente nel periodo estivo, in concomitanza dell’aumento della richiesta associato ai movimenti per le vacanze. A questo andamento possono inoltre sovrapporsi particolari congiunture internazionali (un esempio recente è la guerra in Ucraina). L’andamento mensile dei prezzi netti (escluse IVA e accise) nel nostro Paese per le due tipologie di carburante è mostrato nelle figure 4 e 5. Sono stati considerati l’ultimo anno (da settembre $2022$ a settembre $2023$) e l’anno precedente la pandemia da Covid-$19$ (da settembre $2018$ a settembre $2019$). Oltre a evidenziare la stagionalità, le curve sono utili per far comprendere alle studentesse e agli studenti che, se volessimo costruire una funzione $p(t)$ per riprodurre i grafici in figura 4 e in figura 5, pur avendo la stessa grandezza fisica come variabile indipendente (il tempo), non potremmo utilizzare la stessa espressione analitica della curva di figura 3.
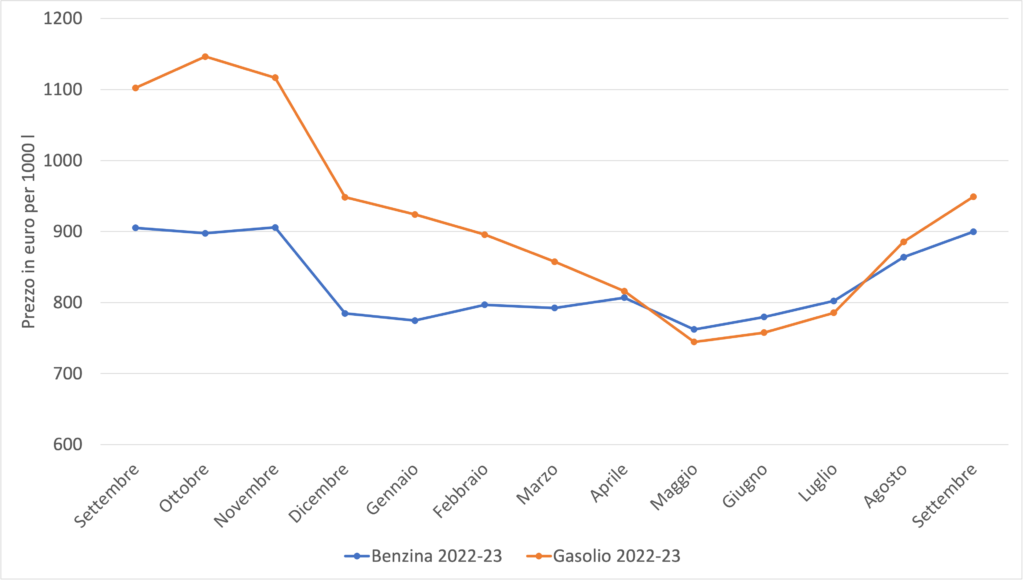
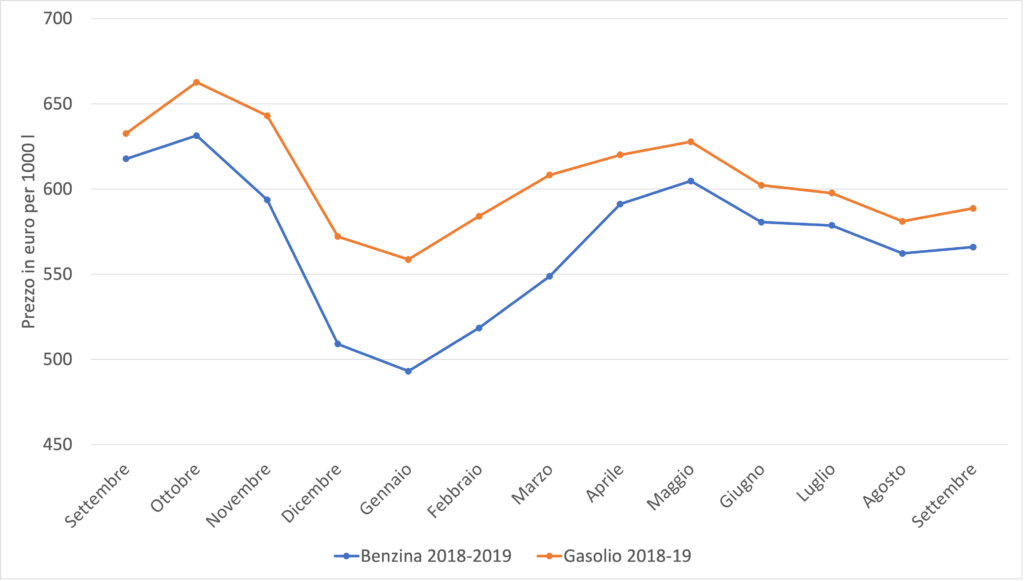
E le variabili $a$, $i$, $p_{n}$ che abbiamo introdotto prima? Il prezzo dipende da loro o dal tempo? Poiché a loro volta $a$, $i$, $p_{n}$ sono funzioni del tempo, queste considerazioni si prestano, in senso lato, a introdurre il concetto di funzione composta.
Appendice
| Anno | Tempo (in anni) | Prezzo netto benzina (euro per $1000$ l) | Prezzo netto gasolio (euro per $1000$ l) |
| $1996$ | $0$ | $249,76$ | $233,53$ |
| $1997$ | $1$ | $262,25$ | $238,18$ |
| $1998$ | $2$ | $229,71$ | $206,05$ |
| $1999$ | $3$ | $258,9$ | $232,69$ |
| $2000$ | $4$ | $380,62$ | $360,69$ |
| $2001$ | $5$ | $352,65$ | $338,39$ |
| $2002$ | $6$ | $330,03$ | $309,91$ |
| $2003$ | $7$ | $339,39$ | $327,54$ |
| $2004$ | $8$ | $379,37$ | $380,35$ |
| $2005$ | $9$ | $453,99$ | $513,23$ |
| $2006$ | $10$ | $507,33$ | $556,44$ |
| $2007$ | $11$ | $518,64$ | $549,66$ |
| $2008$ | $12$ | $588,45$ | $698,92$ |
| $2009$ | $13$ | $464,12$ | $477,8$ |
| $2010$ | $14$ | $572,96$ | $590,22$ |
| $2011$ | $15$ | $639,3$ | $746,46$ |
| $2012$ | $16$ | $759,52$ | $803,53$ |
| $2013$ | $17$ | $713,87$ | $749,95$ |
| $2014$ | $18$ | $673,41$ | $700,22$ |
| $2015$ | $19$ | $529,66$ | $534,5$ |
| $2016$ | $20$ | $455,24$ | $433,51$ |
| $2017$ | $21$ | $524,71$ | $517,35$ |
| $2018$ | $22$ | $582,56$ | $602,5$ |
| $2019$ | $23$ | $561,97$ | $595,32$ |
| $2020$ | $24$ | $444,62$ | $461,87$ |
| $2021$ | $25$ | $604,13$ | $601,48$ |
| $2022$ | $26$ | $943,62$ | $1058,08$ |
| $2023$ | $27$ | $808,39$ | $845,79$ |
1 Decreto Legge $21$/$03$/$2022$ n. $21$ (“decreto Ucraina”), prevede la riduzione delle aliquote di accisa su benzina e gasolio; Legge $10$/$03$/$2023$ n. $23$, prevede l’obbligo di esposizione, da parte dei distributori di carburante, dei prezzi medi su scala locale e nazionale, nonché il rafforzamento dei poteri di controllo del garante per la sorveglianza dei prezzi e disposizioni a sostegno della fruizione del trasporto pubblico.
2 I valori indicati sono relativi al $2023$, secondo i dati del MASE.
