
Il romanzo fantastico Flatlandia – Racconto fantastico a più dimensioni, scritto da Edwin Abbott Abbott nel $1884$, racconta di un mondo bidimensionale popolato da poligoni regolari che si muovono su una superficie piana. In quel mondo tutto scorre tranquillo finché un bel giorno un Quadrato, abitante del regno “piatto”, sogna una Sfera e realizza che può esistere un mondo a tre dimensioni. A questo punto il Quadrato comprende che Flatlandia non esaurisce tutto l’universo ed esprime il desiderio di conoscere il mondo della quarta dimensione, della quinta… e così via.
Fermiamoci qui: già è così difficile trattare con le nostre studentesse e con i nostri studenti le proprietà e le caratteristiche delle figure di geometria piana… figuriamoci il passaggio allo spazio pluridimensionale!
Rimaniamo nelle tre dimensioni. Anche se la geometria 3D modellizza lo spazio in cui viviamo, c’è una bella differenza fra la percezione, l’esperienza quotidiana dello spazio fisico e lo sviluppo e l’elaborazione di concetti geometrici nello spazio astratto e ideale di una teoria matematica.
Diventa di fondamentale importanza saper rappresentare le figure geometriche, vederle attraverso raffigurazioni diverse, muoverle, esplorarle per costruire di esse immagini mentali da manipolare in modo flessibile e competente.
Da questo intento didattico nascono le schede di lavoro che vi propongo, attività rivolte alle studentesse e agli studenti.
La prima attività stimola la riflessione sui triangoli che formano le facce di una piramide; si parte da un semplice foglio di carta di forma quadrata.
Costruisci una piramide
Ci chiediamo se esista una piramide a base quadrata che abbia per facce quattro triangoli rettangoli congruenti.
Prova a costruire la piramide richiesta con la carta. Innanzi tutto osserva che l’angolo retto di ciascuna faccia laterale non può essere adiacente alla base della piramide.
Prendi un foglio di carta quadrato e piegalo lungo le diagonali (figura 1); come sono i quattro angoli, formati dalle diagonali, che hanno il vertice in comune?
Ora tenta di alzare dal piano il centro del foglio per formare una piramide: perché non si riesce?
È dunque evidente che non è possibile costruire una piramide a base quadrata che abbia per facce quattro triangoli rettangoli congruenti.
Prova a eseguire la costruzione con tre facce laterali. Ritaglia uno dei quattro triangolini che si sono formati con le pieghe (figura 2) e avvicina i due lembi del taglio (figura 3); usa del nastro adesivo per chiudere la figura.
Hai costruito una piramide: che tipo di triangolo forma la sua base? Da quali tipi di triangoli sono formate le sue facce laterali?
Sappiamo che le relazioni fra elementi di un solido sono spesso ricondotte allo studio di figure piane, attraverso sezioni del solido. È questo il focus della seconda attività, che analizza le relazioni fra alcuni elementi di un cubo. Lo strumento utilizzato, in questo caso, è l’ambiente 3D di GeoGebra, che consente una manipolazione dinamica del solido. La scheda introduce i comandi necessari alla costruzione.
Esplora le relazioni fra elementi di un cubo nell’ambiente tridimensionale di GeoGebra
Apri l’ambiente Grafici 3D di GeoGebra; nascondi gli assi cartesiani.
Segna due punti $A$ e $B$ sul piano di base e, dal menu per la costruzione dei solidi, seleziona Cubo; fai clic prima sul punto $A$ e poi sul punto $B$. Ottieni lo stesso solido facendo clic prima su $B$ e poi su $A$?
Tieni premuto il tasto destro del mouse sul solido e muovi la figura per osservarla da punti di vista diversi. Costruisci i segmenti $AF$, $AH$ e $HF$ (vedi figura a fianco) e formula un’ipotesi sull’ampiezza dell’angolo $A\widehat{F}H$.
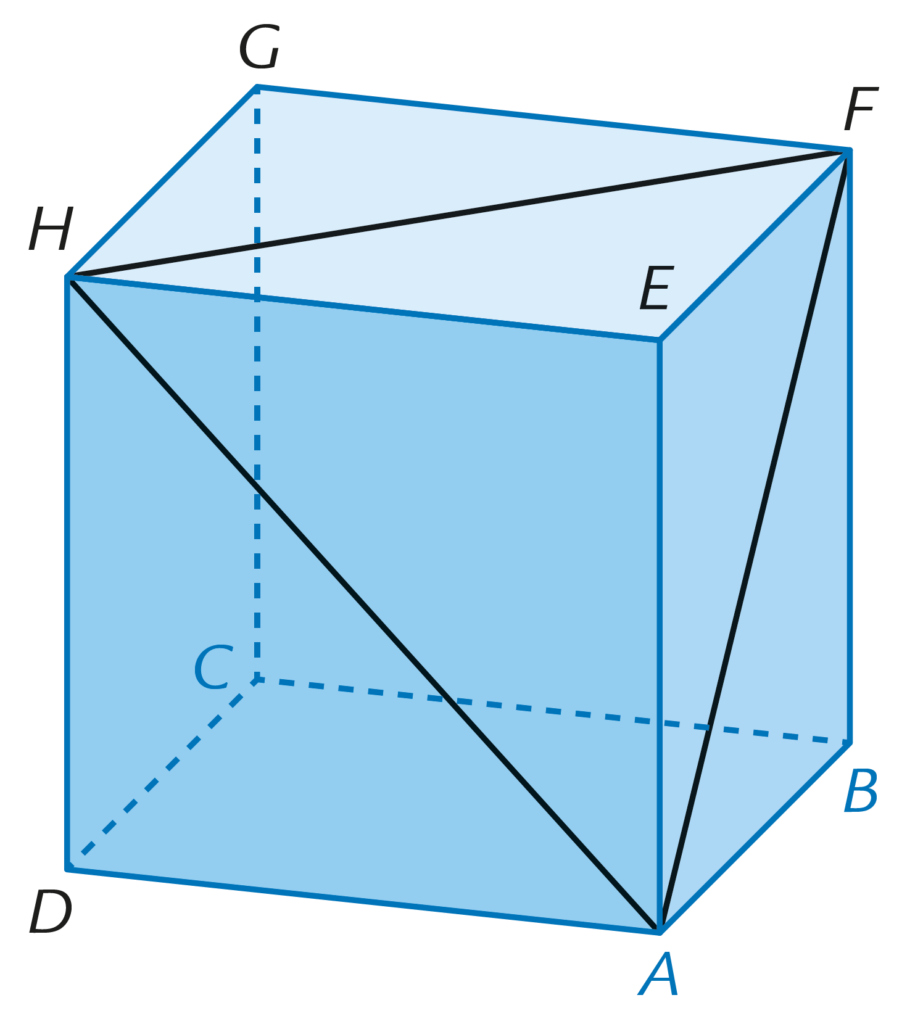
Verifica la correttezza della tua ipotesi attraverso considerazioni geometriche.
- Osserva le tre facce piane che contengono i tre segmenti $AF$, $AH$ e $FH$. Se lo spigolo del cubo misura $l$, che cosa si può dire della misura del segmento $AH$?
- Ricava algebricamente le misure dei segmenti $AF$ e $HF$.
- Come sono i tre segmenti $AF$, $AH$ e $FH$? E perciò come risulta il triangolo $AFH$? Quanto misura dunque l’angolo $A\widehat{F}H$?
Individua ora elementi del cubo che appartengono a uno stesso piano.
- Considera il segmento $GH$ e il punto $B$ e verifica con GeoGebra che esiste un piano che li contiene: seleziona il comando Piano per tre punti e fai clic sui punti $G$, $H$ e $B$. Muovi la figura per rispondere più facilmente alle seguenti domande: quale altro vertice del cubo appartiene al piano che hai disegnato? Quale spigolo?
- Costruisci l’intersezione fra il piano e il cubo utilizzando il comando Interseca due superfici e formula un’ipotesi sulla figura geometrica che viene evidenziata. Verifica la correttezza della tua ipotesi attraverso considerazioni geometriche, riferendoti in particolare alle misure dei lati e delle diagonali di tale figura.
- Sulla base delle considerazioni precedenti si può dire che le rette $HG$ e $HA$ sono perpendicolari?
L’attività precedente evidenzia come GeoGebra 3D sia un potente strumento per la rappresentazione e la manipolazione di figure solide. Insieme ai modellini tridimensionali costruiti con la carta o con bastoncini può fare da potente mediatore nel passaggio dall’esperienza spaziale alla costruzione di una scienza geometrica.
Queste attività di esplorazione sono tratte da “Matematica allo specchio edizione Blu – II biennio e V anno”, il nuovo corso di Matematica edito da Ghisetti e Corvi.

