
Per introdurre il concetto di equazione nella mia classe terza utilizzo abitualmente la rappresentazione grafica tramite le bilance. Spesso i libri di testo offrono già esercizi che utilizzano l’analogia tra bilance ed equazioni ma, per personalizzare l’attività didattica, ho pensato di creare alcuni esercizi, di difficoltà progressiva, legati alla primavera che sta per arrivare.
Il primo esercizio prevede una fioritura di bulbi di tulipano in equilibrio con due sacchi di massa nota:
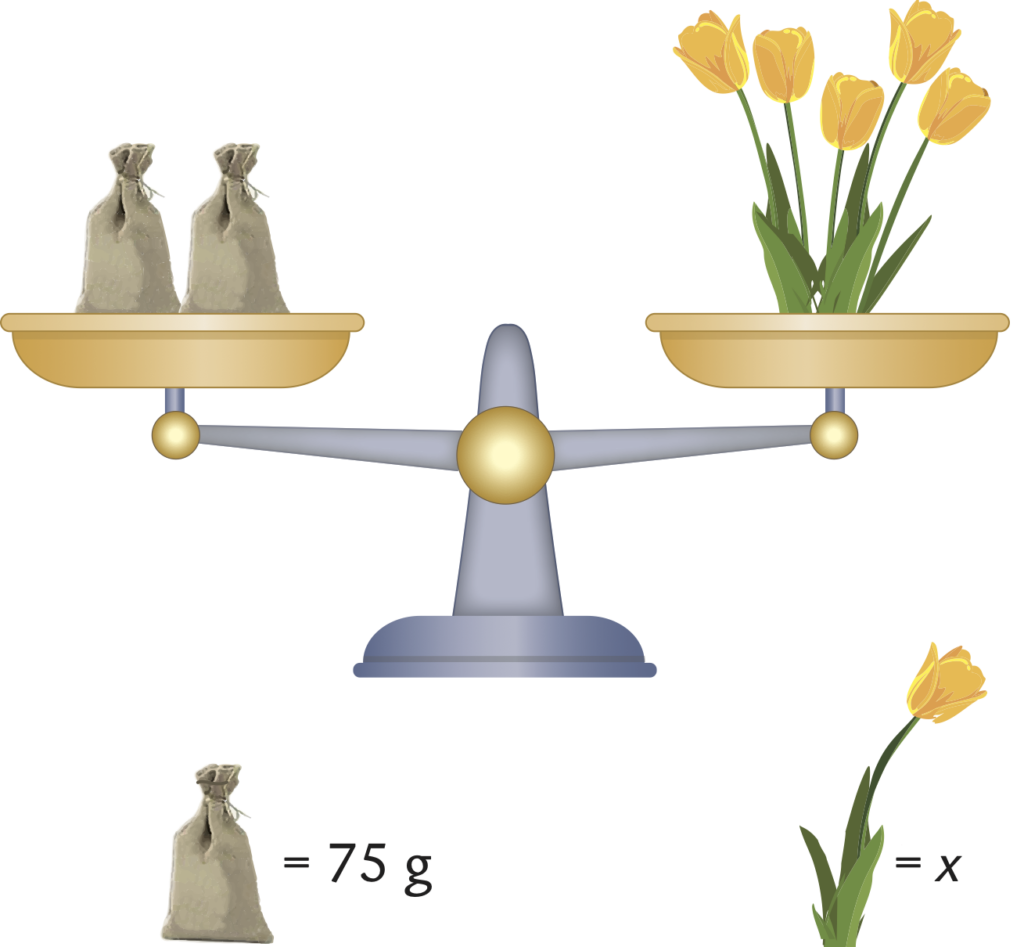
La richiesta è quella di determinare la massa di un tulipano fiorito e l’equazione da risolvere è: $2\cdot 75=5x$ che diventa $150=5x$ e quindi permette di comprendere che, dividendo per $5$ entrambi i termini, un tulipano ha una massa di $30$ g.
La seconda immagine fornita alle mie studentesse e ai miei studenti invece riporta i tulipani su entrambi i piatti della bilancia. Ho anche deciso di cambiare colore per non incappare in fraintendimenti con ciò che era stato identificato nel primo quesito.
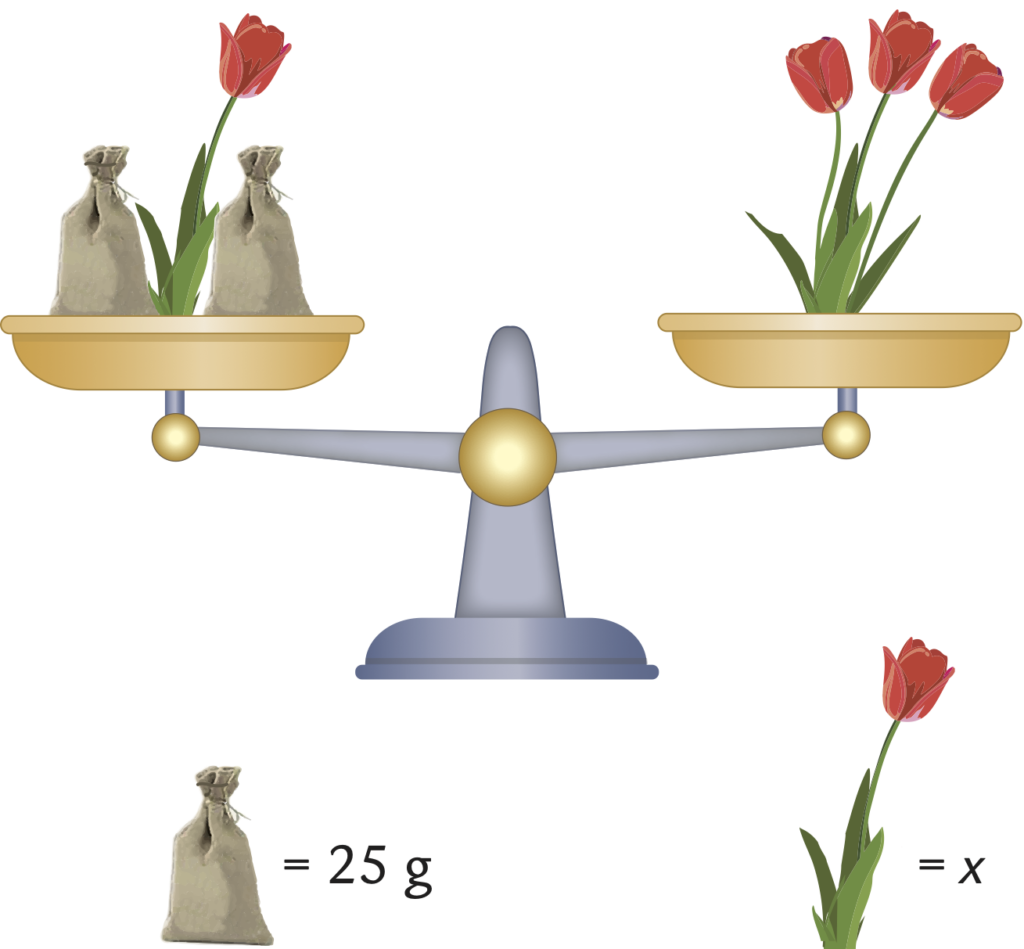
La rappresentazione conduce a formalizzare l’equazione $x+2\cdot 25=3x$ che mi permette di introdurre il concetto del primo principio di equivalenza per cui, togliendo un tulipano da entrambi i piatti, la bilancia rimane in equilibrio e la nostra equazione risulta equivalente a $50=2x$ che, dimezzando entrambi i membri, permette di determinare la massa del tulipano rosso uguale a $25$ g.
Il terzo esercizio proposto inserisce il sacchetto di massa nota anche sul secondo piatto della bilancia, l’incognita su entrambi i piatti e cambia la tipologia di fiore bulboso: il narciso.
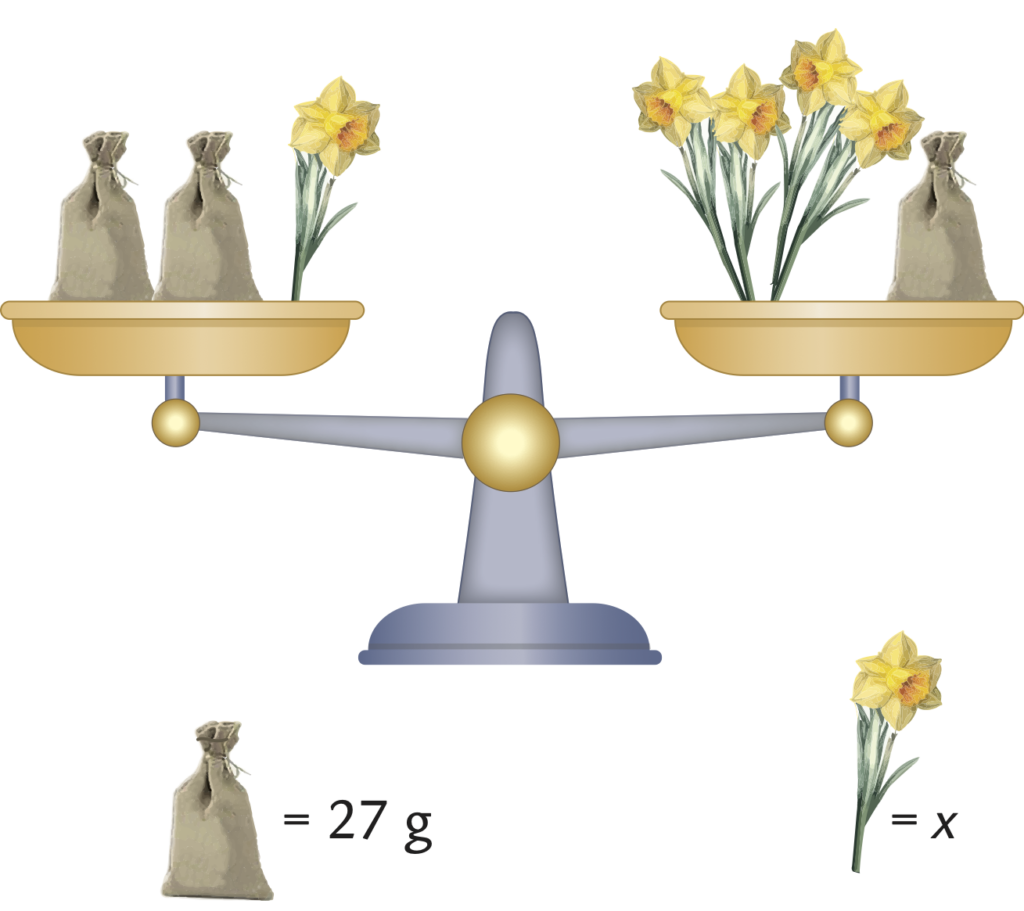
L’equazione che descrive la situazione è $2\cdot 27+x=4x+27$ che, togliendo un sacchetto e un fiore per parte, si semplifica in $27=3x$. Si passa quindi a determinare la massa del bulbo di narciso fiorito in $9$ g, dividendo per tre entrambi i membri.
Gli esempi di utilizzo possono essere ancora molti, proponendo alla classe di creare situazioni simili con disegni personali in cui far comparire fiori e sacchetti su entrambi i piatti della bilancia, variando il numero per poi scrivere l’equazione corrispondente e proporne la soluzione al vicino di banco.
L’utilizzo della bilancia nella risoluzione di semplici equazioni è particolarmente utile nel richiamare la metodologia risolutiva, quando i calcoli si complicano e studentesse e studenti si dimenticano l’esperienza grafica della bilancia a due braccia. Spesso utilizzo anche le mani e le braccia per richiamare tali situazioni, le ragazze e i ragazzi sorridono per il mio gesticolare ma l’importanza dei gesti nella matematica non è da sottovalutare.
