
Siamo ormai al secondo anno di allerta siccità, sempre più marcata per chi abita nel Nord Ovest del Paese. Per parlare di questa emergenza, legata al cambiamento climatico in atto, con la classe terza siamo partiti da una notizia di pochi giorni fa che è facilmente reperibile online: “Siccità, l’Isola dei Conigli sul Garda è raggiungibile a piedi”.
Abbiamo osservato le immagini che mostrano il livello dell’acqua del Lago di Garda, mai stato così basso in inverno da oltre $30$ anni: è inferiore di oltre $50$-$60$ cm rispetto alla media stagionale. L’Isola di San Biagio a Manerba sul Garda, in provincia di Brescia, detta anche Isola dei Conigli, in questi giorni si può raggiungere passeggiando sull’istmo che la collega alla terraferma.
Abbiamo letto che sono in previsione incontri, sia a livello regionale che nazionale, per riflettere sulla situazione e organizzare, nel modo migliore, l’utilizzo delle risorse idriche in quanto a oggi le riserve hanno un deficit del $55\%$ che risulta molto simile a quello dello scorso anno (che era stato del $52\%$).
Ci siamo chiesti come mai la passeggiata verso l’Isola dei Conigli sia possibile e abbiamo provato a quantificare la situazione per cercare di capire meglio l’emergenza.
Il Lago di Garda è il più grande lago d’Italia con una superficie di circa $370$ km$^{2}$ ed è il terzo per profondità (dopo quelli di Como e il Maggiore) con un massimo di $346$ m e una media di $133$ m. Il volume di questo bacino è di $49$ km$^{3}$.
Abbiamo ipotizzato di considerare il lago come un cilindro, nonostante l’effettiva forma del Lago di Garda che nella parte nord si presenta stretto a imbuto mentre a meridione si allarga. Conoscendo il volume e utilizzando il dato della profondità media (trasformato in $0,133$ km), abbiamo verificato l’estensione della sua superficie:
$A_{b}=\dfrac{V}{h}=\dfrac{49}{0,133}\approx368$ km$^{2}$
Siamo passati quindi alla determinazione del raggio di base:
$r=\sqrt{\dfrac{A_{b}}{\pi }}=\sqrt{\dfrac{368}{3,14}}\approx 11$ km
Poi ci siamo chiesti quale quantità di acqua mancasse in questo periodo in seguito alla diminuzione di $60$ cm del livello dell’acqua. La profondità del lago è passata da $133$ m a $132,4$ m (sottraendo i $60$ cm che equivalgono a $0,6$ m) e con questo dato abbiamo determinato il nuovo volume:
$V=A_{b}\cdot h=368\cdot 0,1324=48,7232$ km$^{3}$
La differenza di volume è quindi di $0,2768$ km$^{3}$ che equivalgono a (abbiamo riportato tutti i passaggi per non perderci con gli zeri e abbiamo trasformato anche in notazione scientifica):
$276,8$ hm$^{3}=276800$ dam$^{3}=276800000$ m$^{3}=276800000000$ dm$^{3}=276800000000$ ℓ $=2,77\cdot 10^{11}$ ℓ
e cioè circa $277$ miliardi di litri di acqua.
Questa cifra ci lascia sbalorditi perché $60$ cm non ci sembrano molti ma, rapportati alle dimensioni del bacino del lago, la quantità di acqua determinata è un numero veramente grande e di difficile contestualizzazione in situazioni quotidiane.
Rimanendo sullo studio del Lago di Garda, siamo andati alla ricerca di informazioni sul sito internet dell’Arpa della regione Lombardia e abbiamo scaricato un foglio di calcolo riguardante l’altezza dei principali laghi lombardi nell’anno $2021$. Da quel documento abbiamo creato un grafico a linee che ci ha permesso di analizzare il livello rispetto allo zero idrometrico, che riporto di seguito.
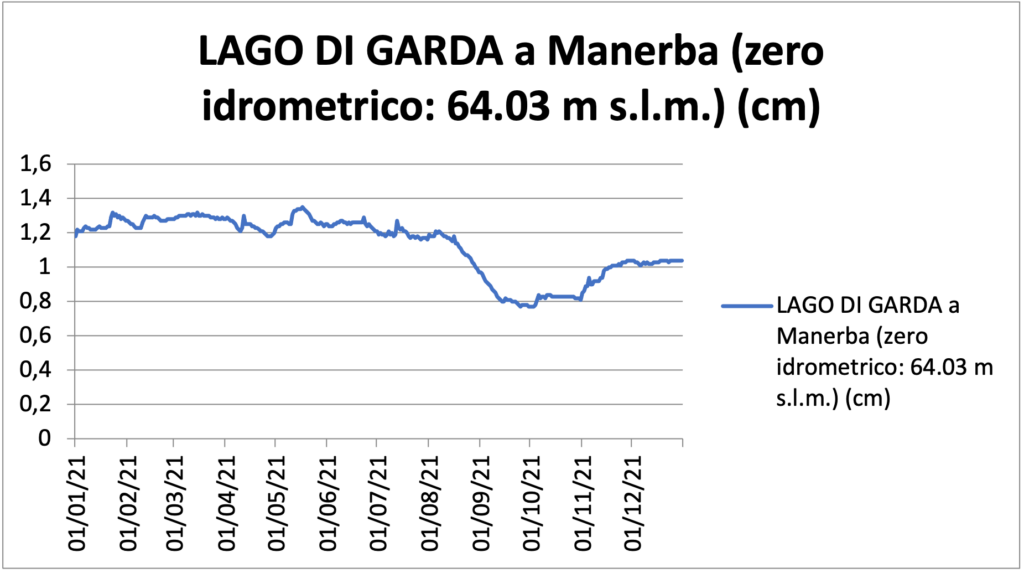
Abbiamo osservato come la discesa più marcata sia iniziata nel mese di agosto per terminare in autunno, rimanendo costante per qualche mese e risalendo solo in periodo invernale.
Siamo curiosi di poter analizzare i dati del $2022$ per evidenziare ciò che le notizie di attualità ci comunicano tramite i mezzi di informazione.
Infine, ci siamo proposti di individuare informazioni riguardo la situazione degli altri grandi laghi italiani facendo riferimento, tra gli altri, al sito internet dell’Ufficio Arpa della regione Piemonte e a quello della Protezione civile della regione Lazio: li utilizzeremo in classe come approfondimento, potrebbero portare a nuove e interessanti considerazioni.
Alice Marro ha parlato di come leggere il mondo che ci circonda con gli occhi della matematica nel webinar “Matematica e attualità”. Guarda il webinar registrato.
