
Il quesito $2$ della Prova INVALSI di Livello $10$ dell’anno $2015$ poneva alle studentesse e agli studenti della classe seconda della scuola secondaria di secondo grado la seguente questione:

Le percentuali di risposte evidenziate dai risultati nazionali sono piuttosto sconfortanti:
- $37,7\%$ di risposte corrette;
- $57,1\%$ di risposte errate;
- $5,2\%$ senza risposta.
Ci si stupisce, ma non più di tanto, di questi risultati; non più di tanto perché ogni insegnante sa quanto sia difficile da parte delle allieve e degli allievi l’approccio ai concetti alla base delle disequazioni.
Per cominciare, una disequazione presuppone una buona conoscenza dell’ordinamento dei numeri nel dominio di riferimento e la considerazione di intervalli numerici come soluzioni. Quindi non uno, due, tre valori numerici, ma infiniti numeri che possono rendere vera la proposizione. E infinite soluzioni, gli insiemi di infiniti numeri, sono qualcosa che spesso sfugge alla consapevolezza delle ragazze e dei ragazzi.
Parliamo, in particolare, di disequazioni di secondo grado: se affrontate e risolte in modo prevalentemente algebrico, la tentazione di ricadere nelle formule risolutive delle equazioni di secondo grado è forte. Suppongo che sia capitata, a molte e a molti di voi, una risposta del tipo $x\geq \pm 1$ alla disequazione $x^{2}-1\geq 0$. Una risposta che rivela una totale incomprensione del significato della domanda, una pura applicazione di regole in un contesto sbagliato.
Un modo per dare senso alla richiesta che pone una disequazione è il riferimento al registro numerico. Una lettura delle operazioni che compongono il polinomio $x^{2}+1$ suggerisce che $x^{2}$ non può essere un numero negativo, qualunque numero reale si sostituisca alla variabile $x$; a maggior ragione $x^{2}+1$ non può che restituire un numero positivo, qualunque sia il valore di $x$. È utile abituare le studentesse e gli studenti a questa analisi già nel momento in cui si trattano le prime formule algebriche. Così facendo, non dovrebbe essere difficile comprendere qual è il segno di polinomi del tipo di $\dfrac{1}{2}x^{2}+0,5$ o $-x^{2}-3$ o ancora $x^{4}+x^{2}+1$.
Naturalmente non tutti i polinomi di secondo grado mantengono un segno costante; si tratta in questi casi di comprendere quali valori numerici sono soluzioni della disequazione e quali no. Non è sbagliato, inizialmente, lavorare su casi di particolari numeri soluzione, prima di ricavare la generalità delle soluzioni. Un approccio possibile potrebbe essere quello descritto dalla seguente scheda di lavoro.
Considera il polinomio di secondo grado $P\left( x\right) =3x^{2}-2x-1$.
Quali valori assume se si danno alla variabile indipendente $x$ i valori $\dfrac{1}{2}$, $-1$, $10$? Prova a rispondere alla domanda con il calcolo mentale.
I risultati che hai ricavato costituiscono informazioni molto precise su tre valori assunti dal polinomio.
Non sempre è necessaria un’informazione così puntuale: talvolta è sufficiente sapere se per certi valori di $x$ il polinomio $P$ assume valori positivi o negativi o nulli.
Per esempio, sai dire se per $x=215$ oppure per $x=-500$ il polinomio $P$ assume un valore positivo? Oppure se il valore di $P$ per $x=-0,2$ è negativo?
Purtroppo il calcolo mentale del valore del polinomio in corrispondenza di questi valori di $x$ non è semplice.
Riscrivi allora l’espressione analitica di $P\left( x\right)$ come prodotto di due fattori di primo grado:
$P\left( x\right) =\left( x-1\right) \left( 1+3x\right) $
e valuta il segno di ciascun fattore.
Completa la tabella seguente, ricordando che non è necessario ricavare il valore di ciascun fattore, ma solo il segno che assume in corrispondenza del valore di $x$ assegnato.
| $x$ | Segno del primo fattore | Segno del secondo fattore | Segno di $P\left( x\right)$ |
| $215$ | |||
| $-500$ | |||
| $-0,2$ |
L’indagine che ho proposto non intende giungere subito alla generalità della cosiddetta tabellina dei segni: il suo scopo è quello di continuare a lavorare con una valutazione numerica. Si sottolinea, in particolare, che la riduzione a fattori di primo grado facilita il calcolo; inoltre non è necessario produrre il valore assoluto del risultato.
Un secondo, formidabile strumento che aiuta alla comprensione dei concetti alla base della soluzione di disequazioni fa uso del registro grafico.
Si tratta di studiare il segno del polinomio $P\left( x\right)$ facendo riferimento al grafico della funzione corrispondente, che può essere disegnato con GeoGebra. L’obiettivo è quello di arrivare alla totalità delle soluzioni di una disequazione del tipo $P\left( x\right) >0$ o $P\left( x\right) <0$, sfruttando l’impatto visivo del colore. Con GeoGebra lo si può fare:
- prendendo un punto $K$ sul grafico;
- costruendo la proiezione $H$ di $K$ sull’asse delle ascisse;
- colorando la proiezione $H$ con un colore diverso a seconda che sia $y_{K} >0$ o $y_{K} <0$.
Se si attiva il comando Traccia attiva per il punto $H$ e si varia con le frecce direzionali la posizione di $K$ sul grafico si possono visualizzare, con colori diversi, gli intervalli del dominio per i quali è $P\left( x\right) >0$ o $P\left( x\right) <0$. Partiamo quindi da questa interpretazione grafica per mostrare che le soluzioni della disequazione sono costituite da intervalli di numeri reali, esprimibili in forma algebrica.
Il file GeoGebra alla base della rappresentazione a colori è piuttosto semplice da costruire; voi insegnanti potete predisporlo in anticipo e lavorare con una lezione dialogata, esplorando con la classe il segno del polinomio di secondo grado in modo dinamico. In alternativa, potete chiedere alle studentesse e agli studenti di costruire le proiezioni colorate e di riflettere sul loro significato.
La scheda seguente prosegue la proposta di lavoro già avviata con l’indagine numerica.
Anziché partire dal valore della variabile indipendente $x$ per ricavare il segno di $P\left( x\right)$, partiamo dall’analisi del segno di $P\left( x\right)$ per trovare valori di $x$.
Esplora la questione con GeoGebra.
Disegna il grafico di $P\left( x\right) =3x^{2}-2x-1$.
Prendi un punto $K$ sul grafico e visualizzane le coordinate; muovi $K$ e osserva i punti del grafico che hanno ordinata negativa; quanti sono? Come sono disposti? Formula una congettura sui valori di $x$ che corrispondono a punti di ordinata negativa.
Verifica ora la tua congettura.
Proietta $K$ sull’asse $x$ nel punto $H=\left( x\left( K\right) ,0\right)$.
Puoi fare in modo che $H$ cambi colore a seconda del segno dell’ordinata di $K$: che sia rosso se $y_{K} >0$ o verde se $y_{K} <0$. A questo scopo apri la casella delle Proprietà di $H$ e seleziona Avanzate/Colori dinamici. Completa le righe relative ai colori con le condizioni indicate nella figura qui sotto.
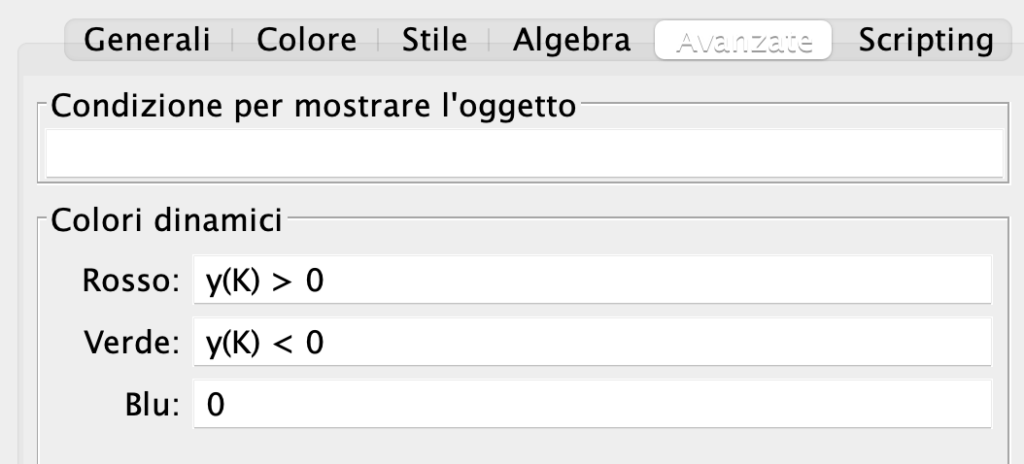
Muovi $K$ sulla parabola usando le frecce direzionali e attiva la traccia di $H$: per quali valori di $x$ il punto $H$ si colora di verde?
Sulla base di queste osservazioni indica per quali valori di $x$ è $P\left( x\right) <0$.
L’esplorazione grafica può essere ripetuta con diverse disequazioni di secondo grado; l’obiettivo è quello di fare in modo che le allieve e gli allievi si abituino a rappresentare graficamente un polinomio di secondo grado, imparino a leggere i segni delle coordinate dei suoi punti comprendendo che eventuali zeri del polinomio fanno da spartiacque fra i valori del dominio che rendono positivo o negativo il polinomio stesso.
Anche le situazioni già esaminate secondo il registro numerico possono essere riprese e valutate nel registro grafico: che cosa comporta, per esempio, il fatto che il polinomio $x^{2}+1$ non abbia zeri? Come si evidenzia, graficamente, che è positivo per qualunque valore reale della variabile $x$?
Solo dopo aver ben compreso il significato di ciò che si sta cercando quando si risolve una disequazione di secondo grado e su quali strumenti ci si può basare per risolverla, si può arrivare alla formalizzazione dei risultati. Con la consapevolezza che, per comprendere, basta lo schizzo grafico di una parabola che riporti le informazioni essenziali: concavità e zeri. E con un metodo di lavoro che può essere trasferito anche ad altri tipi di disequazioni, quali le goniometriche o le esponenziali.
Questa attività di esplorazione è tratta da “Matematica allo specchio”, il nuovo corso di Matematica per la scuola secondaria di secondo grado edito da Ghisetti e Corvi.
