Le radici sono uno dei primi concetti matematici complessi che si incontrano alla scuola secondaria di primo grado; da bravi numeri irrazionali sono un po’ disobbedienti, impossibili da scrivere in modo completo; eppure, sorprendentemente, si possono disegnare e posizionare in modo preciso sulla retta dei numeri.
L’attività che vi propongo è un grande classico e un’ottima occasione per usare contemporaneamente l’aritmetica e la geometria; per realizzarla ci serviranno squadra e compasso.
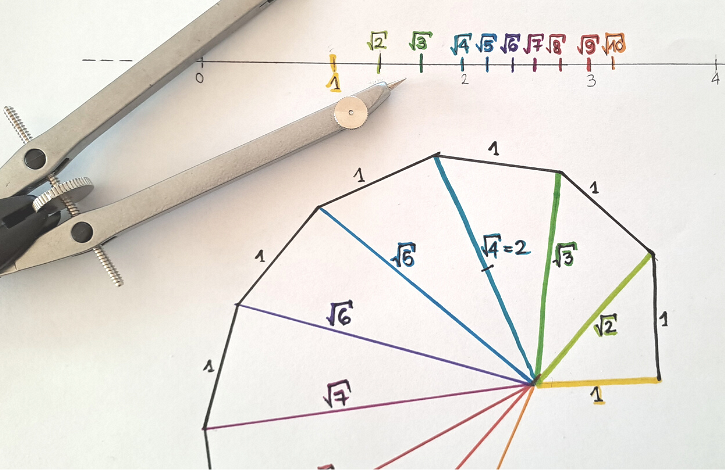
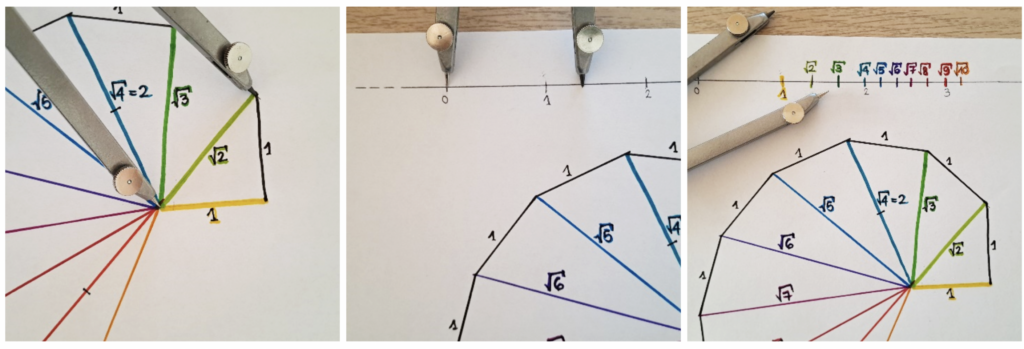
Su un foglio bianco tracciamo una retta, apriamo il compasso a piacere e usiamo questa apertura come unità di misura “$u$” per segnare i primi numeri naturali sulla retta. In corrispondenza del numero $1$ tracciamo un segmento lungo $1u$ perpendicolare alla retta, poi colleghiamo l’estremo libero di questo segmento con il punto $0$. In questo modo avremo ottenuto un triangolo rettangolo isoscele con i cateti lunghi $1u$; grazie al teorema di Pitagora sappiamo che l’ipotenusa misura $\sqrt{2}u$; con l’aiuto del compasso possiamo riportare questa misura in modo esatto sulla retta iniziale.
Similmente, iterando i seguenti passaggi, possiamo disegnare tutte le radici dei numeri naturali:
- tracciare un segmento perpendicolare all’ipotenusa del triangolo precedente;
- riportare la misura di $1u$ con il compasso;
- tracciare l’ipotenusa del nuovo triangolo rettangolo.

Con questo procedimento otterremo una costruzione chiamata “spirale di Teodoro”. Le ipotenuse utilizzate per costruirla rappresentano tutte le radici dei numeri naturali; infatti, per il teorema di Pitagora, la misura della $\left( n+1\right) $-esima ipotenusa sarà $\sqrt{\sqrt{n}^{2}+1^{2}}=\sqrt{n+1}$.
Con l’aiuto del compasso si potranno riportare tutte le radici ottenute sulla linea dei numeri e sarà anche semplice verificare che le radici dei quadrati perfetti corrispondono a numeri naturali.
Naturalmente, la costruzione può essere realizzata anche con GeoGebra. Si parte da un segmento lungo $1$, poi si ripetono i seguenti passaggi:
- retta perpendicolare al segmento e passante per un suo estremo
- circonferenza con centro nello stesso estremo e raggio $1$
- punti di intersezione tra la circonferenza e la retta
- segmento condotto dal punto appena individuato al centro della spirale

Possiamo così sfidare le nostre classi a disegnare il maggior numero possibile di passaggi, a personalizzare nei modi più artistici le proprie spirali o, ancora, chiedere di prevedere quale sarà l’ultimo passaggio che si riesce a disegnare senza sovrapporsi ai precedenti per poi verificare le ipotesi proseguendo la costruzione.
