
Il problema che propongo qui è la rielaborazione di un quesito della Prova INVALSI 2016 per gli studenti della classe seconda della scuola secondaria di secondo grado. Vi sarete accorti che utilizzo spesso questo metodo, cioè scelgo un testo tra i numerosi quesiti delle Prove INVALSI e lo trasformo nel modo che mi sembra più opportuno da proporvi: nell’ambito delle attività che vi sto descrivendo e come ho già sottolineato più volte, l’obiettivo è quello che possiate avere a disposizione un problema piuttosto aperto, cioè risolubile in più di un modo e non riducibile all’esecuzione di calcoli ma che richieda esplicitamente argomentazioni scritte, giustificazioni o riflessioni personali, eventualmente sviluppabili in questioni successive.
Ovviamente, rendendo un quesito più aperto e un po’ più complesso, il mio consiglio è quello di utilizzarlo per un’attività a gruppi, perché la collaborazione di più menti rende più facile l’emergere di strategie e argomentazioni differenti, che voi insegnanti potrete sollecitare e apprezzare in fase di confronto e discussione di classe: in questo modo riuscirete a potenziare l’inventiva dei ragazzi, la loro capacità di scelta e l’abitudine a non essere troppo ancorati a formule e procedimenti noti.
Ecco il testo del problema1:
Un quadrato è formato da due quadrati $A$ e $B$ e da un poligono $C$, come mostrato in figura.
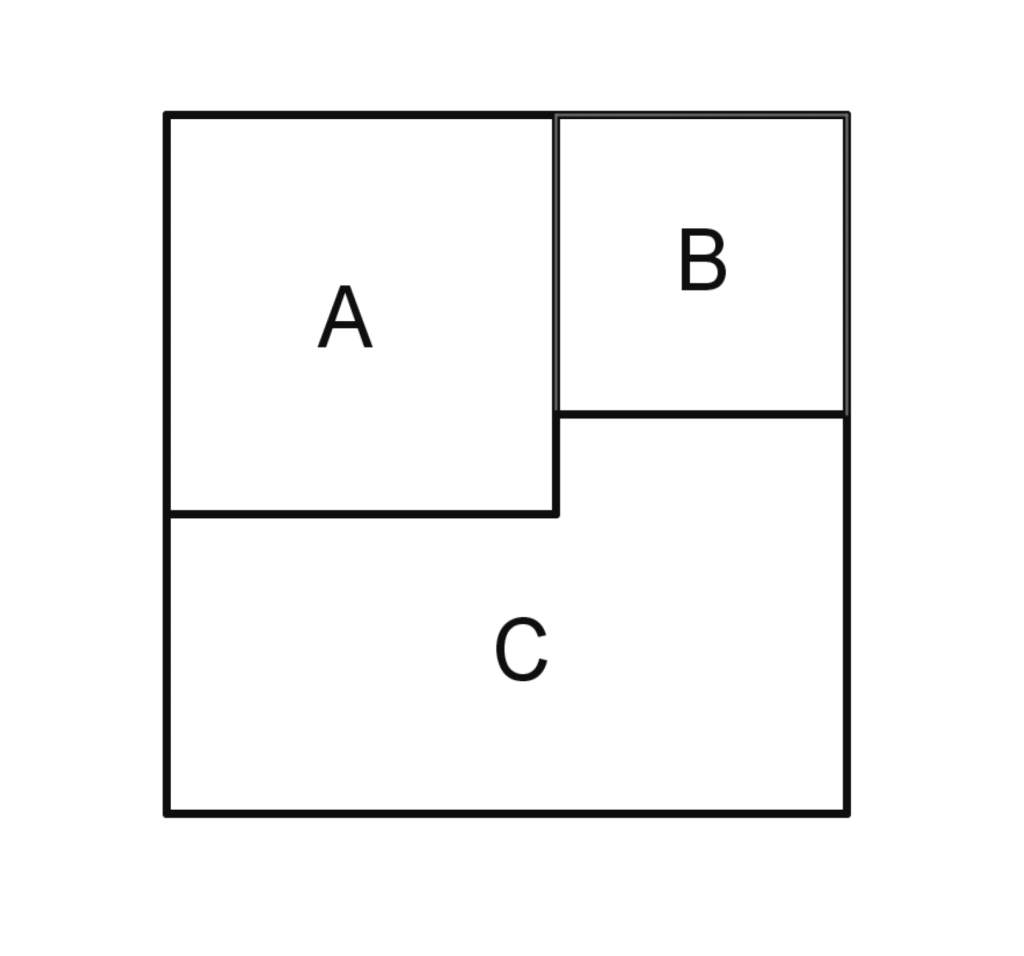
L’area di $A$ è $16$ e quella di $B$ è $9$.
Quali misure puoi ottenere da questi dati? (lati, perimetri, aree, …)
Giustifica i tuoi calcoli con disegni o spiegazioni.
L’attività è proponibile a partire dalla classe prima della secondaria di primo grado, perché la semplicità delle misure consente di procedere in modo elementare, anche se occorre un po’ di iniziativa per dare i nomi più opportuni agli elementi in gioco. Situazioni di questo tipo, che richiedono ai ragazzi un po’ di iniziativa nel denominare i segmenti della figura assegnata o meglio ancora, nel nostro caso, le loro misure, potrebbero potenziare il processo di nominalizzazione, cioè della scelta della nomenclatura più adatta per affrontare il problema: di solito questa fase non è presente, perché ci si limita ad assegnare agli studenti procedimenti da svolgere, con indicazioni già prescritte; tuttavia, come sapete, si tratta di un momento importante, perché mette in gioco e dunque sviluppa iniziativa e capacità decisionali.
Il testo potrebbe destare qualche perplessità nei ragazzi, perché non è usuale in un problema l’assenza di unità di misura, tuttavia ci si rende conto che per rispondere al quesito tale informazione non è necessaria e può essere interessante, se non emerge spontaneamente, farlo notare ai ragazzi nel momento che riterrete più opportuno.
Ecco per esempio come si potrebbero nominare le misure dei vari segmenti nella figura proposta:
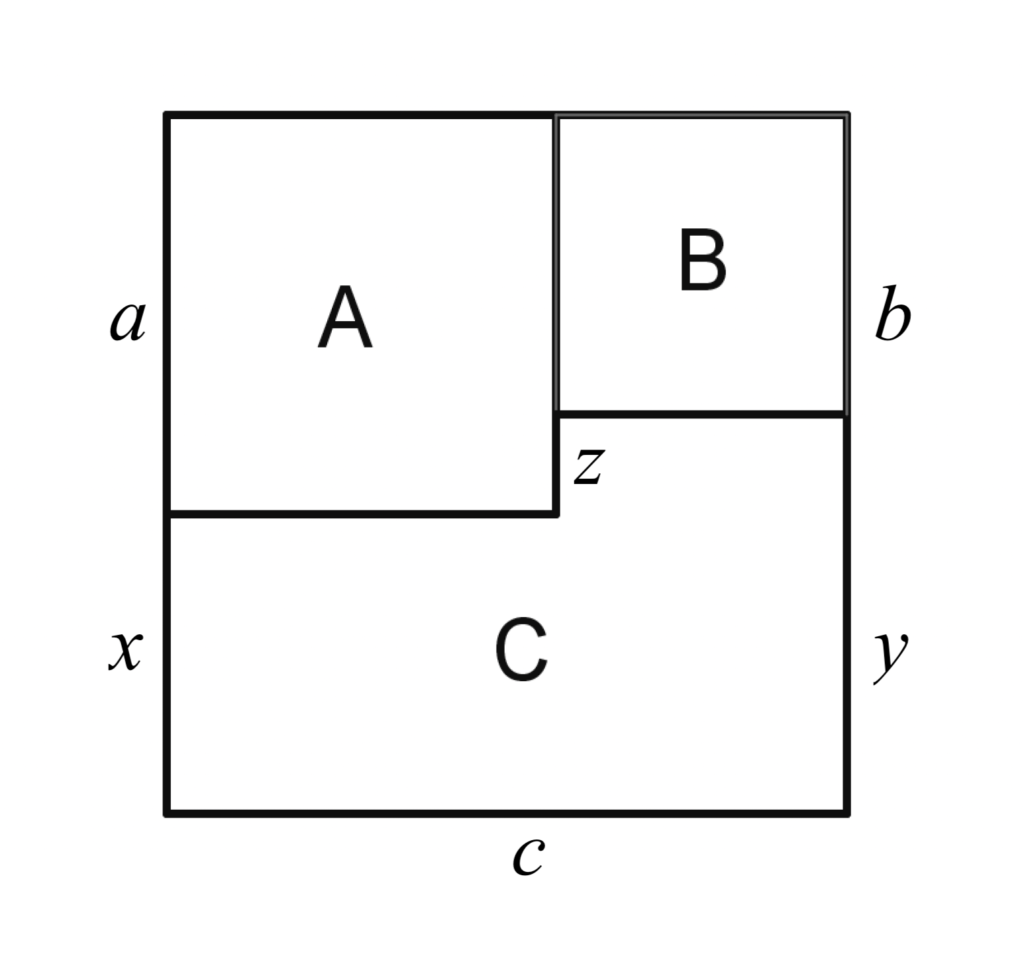
Con tali indicazioni si ottengono subito le uguaglianze che seguono:
- il lato di $A$ misura $a=\sqrt{16}=4$;
- il lato di $B$ misura $b=\sqrt{9}=3$.
È evidente che qui, sia nel caso del lato del quadrato $A$ che del quadrato $B$, non è necessario conoscere il significato della radice quadrata di un numero, perché basta aver chiara la relazione tra lato e area di un quadrato: nel nostro caso si trova intuitivamente il numero il cui quadrato è $16$ oppure $9$. E dunque qualcuno potrà scrivere semplicemente:
- $a=4$ perché $a^{2}=16$;
- $b=3$ perché $b^{2}=9$.
Il lato del quadrato “grande” è la somma del lato del quadrato $A$ e del lato del quadrato $B$, dunque $c=4+3=7$.
La misura $x$ del lato di $C$ si ottiene sottraendo alla misura del lato del quadrato grande la misura del lato del quadrato $A$, dunque $x=7-4=3$.
Oppure, in altro modo, dato che si tratta di un quadrato e dunque ha i lati congruenti, da $c=a+x=a+b$, si ottiene $x=b=3$. Osservo subito che per ottenere questa uguaglianza non occorre far ricorso a passaggi algebrici particolari (citare il primo principio di equivalenza delle equazioni, in questo caso, sebbene corretto, sarebbe davvero eccessivo!) perché si tratta di riconoscere una semplice ed elementare proprietà aritmetica, la seguente: se ad $a$ aggiungo $x$ e ottengo lo stesso risultato che ho aggiungendo ad $a$ il numero $b$, allora $x$ e $b$ sono certamente uguali! Riuscire a esprimere verbalmente questa proprietà non è del tutto scontato ma come sapete occasioni di questo tipo, in cui l’interpretazione delle lettere in gioco è facilitata dal collegamento a una figura familiare e a numeri semplici come quelli proposti, possono essere utili per favorire il passaggio consapevole dal pensiero aritmetico a quello algebrico, prima che il tecnicismo dell’algebra copra del tutto i significati a essa collegati.
Il lato di $C$ con misura $y$ si ottiene, in modo analogo, sottraendo al lato del quadrato grande il lato del quadrato $B$, dunque $y=7-3=4$. Procedendo come prima, si può scrivere $c=b+y=a+b$, da cui si ottiene $y=a=4$.
Il lato di $C$ con misura $z$ è il lato del quadrato $A$ meno il lato del quadrato $B$, dunque $z=a-b=1$.
Il perimetro di $C$, tenendo conto delle uguaglianze ottenute ($a=y=4$, $b=x= 3$), misura dunque: $p=a+b+c+x+y+z=22$.
I perimetri dei due quadrati $A$ e $B$ misurano invece $16$ e $12$ rispettivamente.
Passiamo ora a considerare l’area di $C$: essa si può calcolare nei due modi seguenti come somma di aree di rettangoli diversi, facilmente interpretabili in figura:
Area di $C=x\cdot c+z\cdot b=3\cdot 7+1\cdot 3=24$
Area di $C=x\cdot a+y\cdot b=3\cdot 4+4\cdot 3=24$
Ovviamente si può procedere anche più semplicemente, calcolando l’area di $C$ come differenza tra l’area del quadrato grande e l’area di $A$ e $B$, cioè:
Area di $C=c^{2}-a^{2}-b^{2}=49-16-9=24$
Un’osservazione curiosa riguarda il confronto tra il perimetro della figura “$A+B$”, unione dei due quadrati $A$ e $B$, e il perimetro del poligono $C$: si riconosce facilmente, in base alle uguaglianze trovate, che hanno lo stesso perimetro, $22$, tuttavia le loro aree sono diverse, cioè $25$ ($=16+9$) e $24$ rispettivamente!
Una nota ulteriore potrebbe riguardare il tipo di poligoni in gioco: il quadrato assegnato è costituito dai due quadrati $A$ e $B$ e dal poligono $C$, che è un esagono, non certo regolare ma con la caratteristica di avere tutti gli angoli retti, dunque sia $A$ che $B$ che $C$ sono poligoni nei quali tutti gli angoli sono retti.
Le osservazioni che ho proposto non sono tutte richieste ma, eventualmente insieme ad altre, potrebbero emergere spontaneamente o essere sollecitate da voi insegnanti, sempre nell’ottica di promuovere riflessioni personali e non stereotipate, collegate agli aspetti aritmetici o geometrici che i ragazzi possono cogliere liberamente e che si devono sentire spronati a formulare, argomentare, discutere e condividere con i compagni.
1 Il problema è una rielaborazione del quesito D9 della Prova INVALSI 2015-2016 per la classe seconda della scuola secondaria di secondo grado: la domanda aperta qui proposta e la richiesta di giustificazioni sostituiscono la richiesta di calcolo del solo perimetro del poligono $C$ nel quesito ministeriale.
