Ogni inizio d’anno a Mondovì, cittadina che confina con il Comune in cui si trova la scuola dove insegno Matematica e Scienze, si organizza il raduno aerostatico internazionale dell’Epifania. Siamo alla trentaseiesima edizione e, anche in questa occasione, i cieli si sono riempiti di coloratissime mongolfiere, alcune dalle forme particolarmente stravaganti.
Ho deciso di trarre ispirazione da questo evento per introdurre il concetto di solidi di rotazione in una classe terza della scuola secondaria di primo grado. Gli studenti hanno già familiarità con le caratteristiche principali dei solidi geometrici e hanno sperimentato la costruzione dei relativi sviluppi piani (tetraedro, cubo, ottaedro ecc.).
Per passare alla geometria dei solidi di rotazione, è fondamentale partire da una definizione rigorosa:
Si definisce solido di rotazione un solido ottenuto facendo ruotare una figura piana attorno a un asse fisso (asse di rotazione) appartenente allo stesso piano della figura.
Il processo logico che abbiamo seguito in classe è il seguente:
- si individua una figura bidimensionale (per esempio semicerchio, trapezio, rettangolo);
- si sceglie un asse di rotazione;
- la rotazione completa della figura attorno all’asse genera un volume nello spazio.
Abbiamo quindi identificato i principali esempi:
- Sfera → semicerchio ruotato attorno al diametro
- Cilindro → rettangolo ruotato attorno a uno dei lati verticali
- Cono → triangolo rettangolo ruotato attorno a un cateto
Siamo passati all’analisi tecnica di una mongolfiera, partendo da un disegno semplificato. Quali solidi la compongono? Essenzialmente, una sfera e un tronco di cono.
Per visualizzarla correttamente, abbiamo proceduto alla rappresentazione di una sezione verticale sul piano cartesiano:
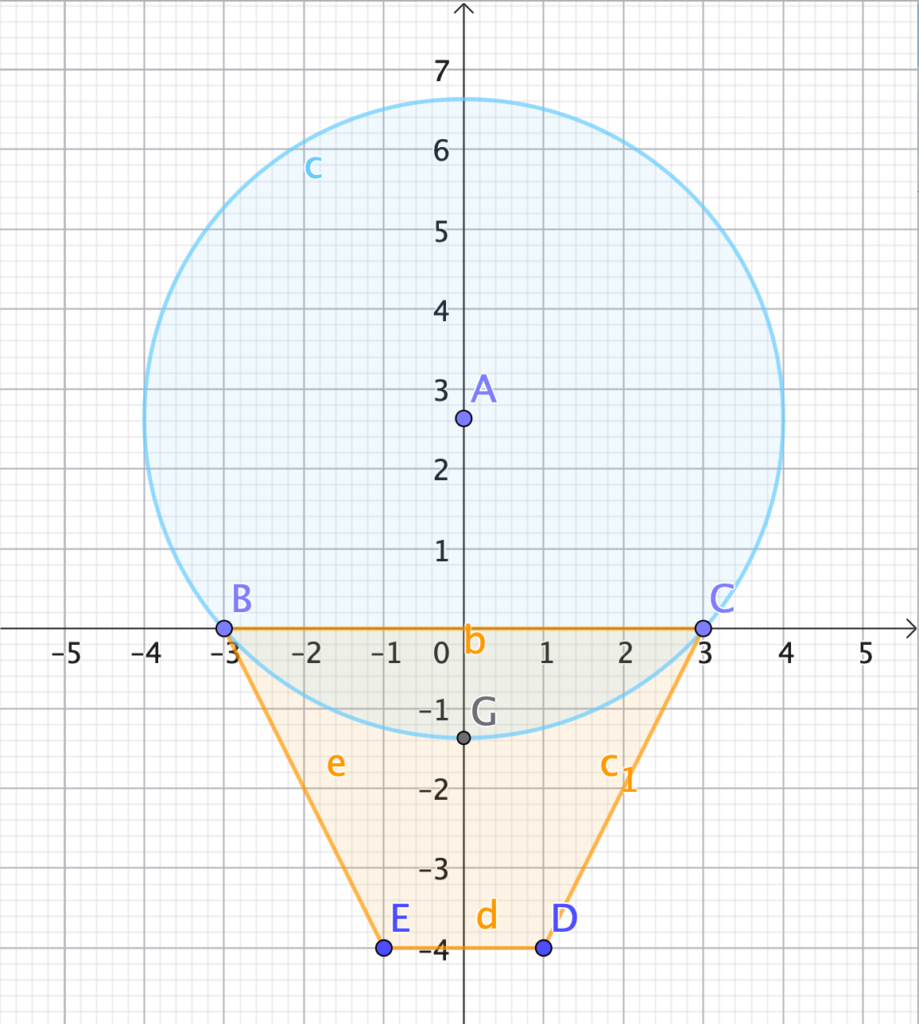
- abbiamo disegnato un trapezio isoscele con base maggiore di $6$ unità ($u$), base minore di $2u$ e altezza $4u$;
- abbiamo posizionato la figura in modo simmetrico rispetto all’asse delle ordinate ($y$), con la base maggiore rivolta verso l’alto;
- utilizzando il compasso, abbiamo tracciato una circonferenza di raggio $4u$ passante per gli estremi della base maggiore.
L’immagine, realizzata con GeoGebra, è facilmente riproducibile sul quaderno. Ecco i punti chiave utilizzati: $A\left( 0;+2,6\right) $, $B\left( -3;0\right)$, $C\left( +3;0\right)$, $D\left(+1;-4\right)$, $E\left( -1;-4\right)$
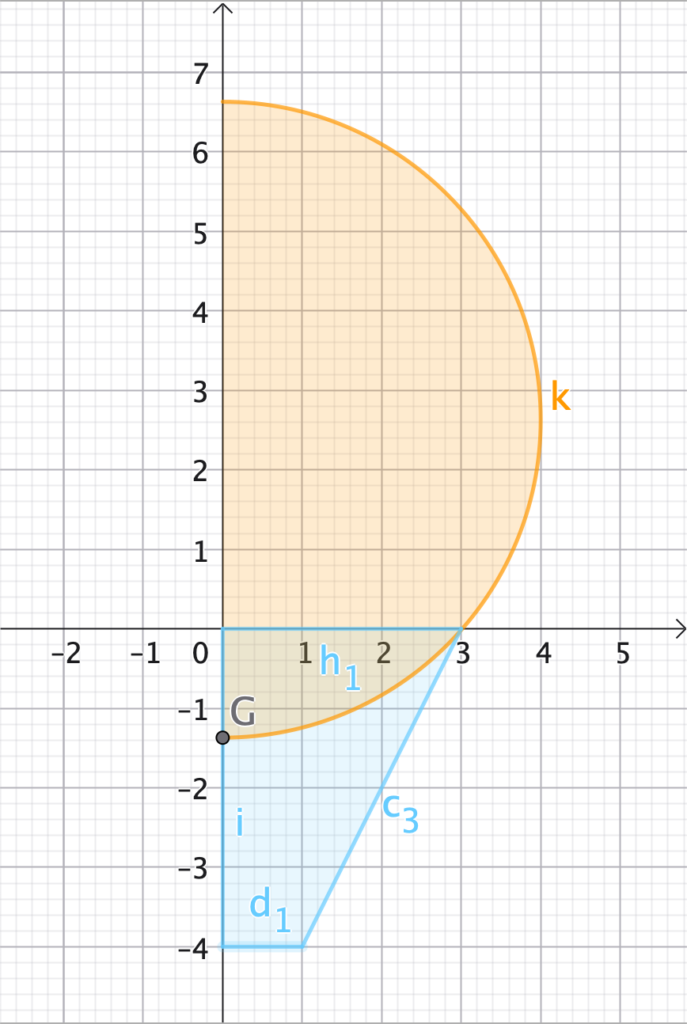
Per comprendere come si origini il solido, è necessario individuare le figure piane che ruotano attorno all’asse $y$. “Tagliando” la sezione lungo l’asse di simmetria, otteniamo:
- un semicerchio (che genererà la sfera);
- un trapezio rettangolo (che genererà il tronco di cono).
L’unione di queste due figure in rotazione dà vita al solido della nostra mongolfiera.
L’attività si presta a evoluzioni successive, ma non abbiamo ancora affrontato le formule per il calcolo dei volumi e delle superfici dei solidi; quindi, ho proposto a studentesse e studenti una sfida sulla sezione piana:
Determina l’area complessiva della sezione verticale. Sapendo che la porzione di cerchio che si sovrappone al trapezio è circa il $10\%$ dell’area totale del cerchio, calcola l’area della figura ricordando di sottrarre la parte sovrapposta dalla somma delle due aree (per evitare di contarla due volte).
Ecco i calcoli svolti:
$A_{cerchio}=\pi r^{2}=\pi \cdot 4^{2}=16\pi\approx 50,24u^{2}$
$A_{trapezio}=\dfrac{\left( B+b\right) \cdot h}{2}=\dfrac{\left( 6+2\right) \cdot 4}{2}=\dfrac{8 \cdot 4}{2}=16u^{2}$
$10\%$ di $A_{cerchio }=0,1 \cdot 50,24=5,02u^{2}$
$A_{totale}=A_{cerchio}+A_{trapezio}-10\%A_{cerchio}=50,24+16-5,02=61,22u^{2}$
La proposta, in questo periodo dell’anno scolastico, si conclude qui ma sarà possibile proseguire con altre richieste quando saranno affrontati tutti gli argomenti legati alla geometria solida. Le richieste potrebbero allora essere legate al volume e alla superficie di tessuto necessaria per creare questa mongolfiera.
Chiedo però alle studentesse e agli studenti, come compito, di pensare a un altro oggetto che possa essere costruito come solido di rotazione composto, di disegnarne sul quaderno la sezione piana verticale e pensare alla sua rotazione nello spazio.
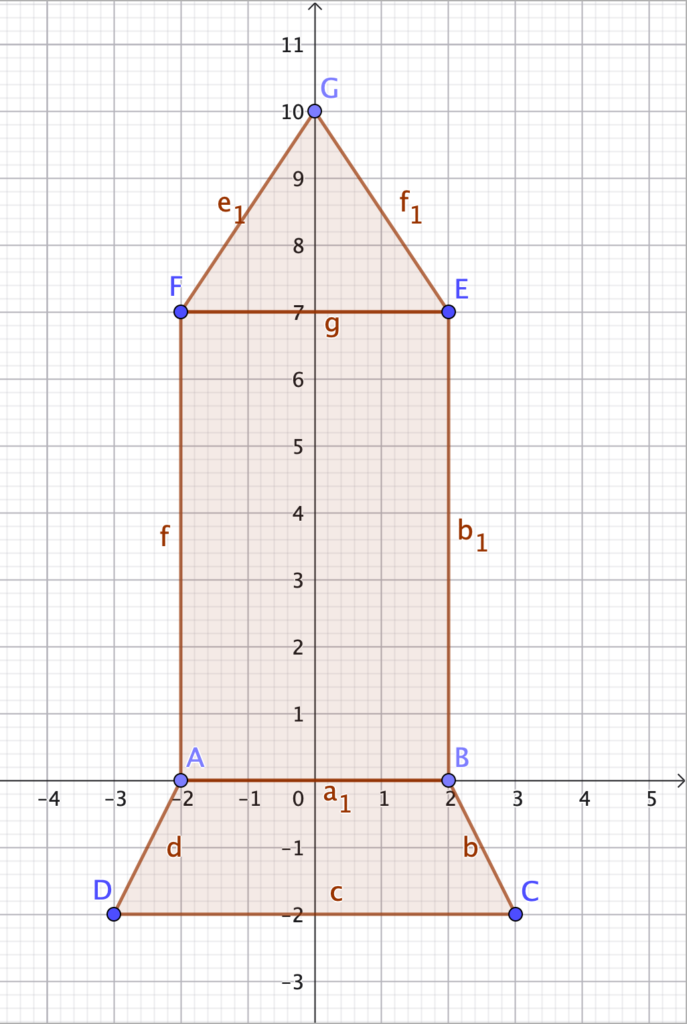
Così, parlando di spazio, mi viene in mente un razzo (costituito da trapezio isoscele, rettangolo e triangolo isoscele) che vi riporto solo come bozza di nuova attività sul piano cartesiano.