
Nell’articolo precedente ho introdotto e analizzato i concetti di TAN e TAEG partendo dall’esempio concreto dell’acquisto di uno smartphone a rate. Alcuni aspetti meritano un ulteriore approfondimento: perché, alla fine del periodo, l’importo complessivamente restituito non coincide con il capitale finanziato aumentato del TAEG? In ciascuna rata, a quanto ammonta la quota di capitale restituito e a quanto la quota di interessi? È possibile avere rate di importo diverso a parità di capitale finanziato e di TAEG? Per rispondere a queste domande introdurrò un altro concetto fondamentale in matematica finanziaria, cioè quello di piano di ammortamento.
Il costo complessivo di un finanziamento
Riprendiamo l’esempio del nostro smartphone da $1000$ euro acquistato con rate mensili a un TAEG del $2,2\%$ e strutturiamo un nuovo compito di realtà da sottoporre alle nostre studentesse e ai nostri studenti.
- Utilizza la funzione del foglio di calcolo per calcolare l’importo della rata mensile, nel caso in cui il rimborso avvenga in un anno; ripeti il calcolo nel caso in cui il debito sia estinto in $2$, $3$ e $4$ anni.
- Tenendo presente che il costo complessivo del finanziamento è dato dall’importo della singola rata per il numero di rate, calcola il costo complessivo del finanziamento in ciascun caso e stabilisci se esso aumenta linearmente con il tempo.
- Determina il costo complessivo se l’estinzione del debito avviene, per ciascuna durata, a) in un’unica soluzione, b) con rate semestrali, c) con rate mensili.
- Riporta in un grafico il costo complessivo, per una durata fissata, in funzione del numero di rate e commenta i risultati.
- Determina, in percentuale rispetto al capitale finanziato, il costo del finanziamento nei casi in esame.
Lo scopo di questa attività è quello di mostrare che il costo complessivo di un finanziamento dipende, oltre che da quanto tempo impieghiamo per rimborsare il capitale, anche da quanto frequentemente versiamo le rate. Si osserva infatti che, a fronte di un prestito di $1000$ euro, dovremo restituire complessivamente $1022$ euro se paghiamo un’unica rata, $1016,44$ euro se paghiamo ogni sei mesi, $1011,84$ euro se rimborsiamo il capitale con cadenza mensile. Il motivo per cui ciò avviene è che gli interessi vengono calcolati sull’intera somma finanziata solo per la prima rata; il calcolo successivo avviene invece sul capitale residuo da restituire, che va via via diminuendo nel tempo.
Come è fatta una rata
Per analizzare la distribuzione degli interessi nel tempo e la composizione della rata, introduciamo il concetto di piano di ammortamento, che rappresenta nel dettaglio la modalità di restituzione di un capitale preso in prestito. Esso può essere schematizzato mediante una tabella costituita dalle seguenti voci/colonne:
- periodo: è rappresentato da un numero progressivo, da $1$ a $n$, con $n=$ numero totale di rate del finanziamento (per esempio, nel caso dello smartphone da pagare in $2$ anni mediante rate mensili, $n=24$);
- rata: è l’importo pagato nel periodo;
- quota interessi: è la parte della rata relativa all’interesse sul debito residuo precedente, cioè l’ammontare degli interessi sul capitale ancora da restituire;
- quota capitale: rappresenta la parte del capitale ottenuto in prestito che viene restituita nel periodo;
- debito residuo: è il capitale ancora da rimborsare dopo il pagamento del periodo.
La tabella che segue mostra uno dei possibili piani di ammortamento per il nostro smartphone da $1000$ euro in un anno con TAEG $2,2\%$ e può essere facilmente ottenuta anche dalle studentesse e dagli studenti con l’aiuto di un chatbot che fornisce le istruzioni dettagliate per la costruzione del piano da inserire direttamente nel foglio di calcolo che si vuole utilizzare1.
| Periodo | Importo Rata | Quota interessi | Quota capitale | Debito residuo |
| $1$ | $84,33$ | $1,83$ | $82,50$ | $917,5$ |
| $2$ | $84,33$ | $1,68$ | $82,65$ | $834,86$ |
| $3$ | $84,33$ | $1,53$ | $82,80$ | $752,06$ |
| $4$ | $84,33$ | $1,38$ | $82,95$ | $669,11$ |
| $5$ | $84,33$ | $1,23$ | $83,10$ | $586$ |
| $6$ | $84,33$ | $1,07$ | $83,26$ | $502,75$ |
| $7$ | $84,33$ | $0,92$ | $83,41$ | $419,34$ |
| $8$ | $84,33$ | $0,77$ | $83,56$ | $335,78$ |
| $9$ | $84,33$ | $0,62$ | $83,71$ | $252,06$ |
| $10$ | $84,33$ | $0,46$ | $83,87$ | $168,2$ |
| $11$ | $84,33$ | $0,31$ | $84,02$ | $84,18$ |
| $12$ | $84,33$ | $0,15$ | $84,18$ | $0$ |
Confronto tra piani di ammortamento
L’esempio sopra riportato costituisce in realtà solo una delle possibili modalità di restituzione di un prestito, nella quale l’importo della rata si mantiene invariato per tutta la durata del finanziamento. È utile spiegare alle nostre studentesse e ai nostri studenti che esistono diverse tipologie di piani di ammortamento, tra i quali vale la pena menzionare i seguenti:
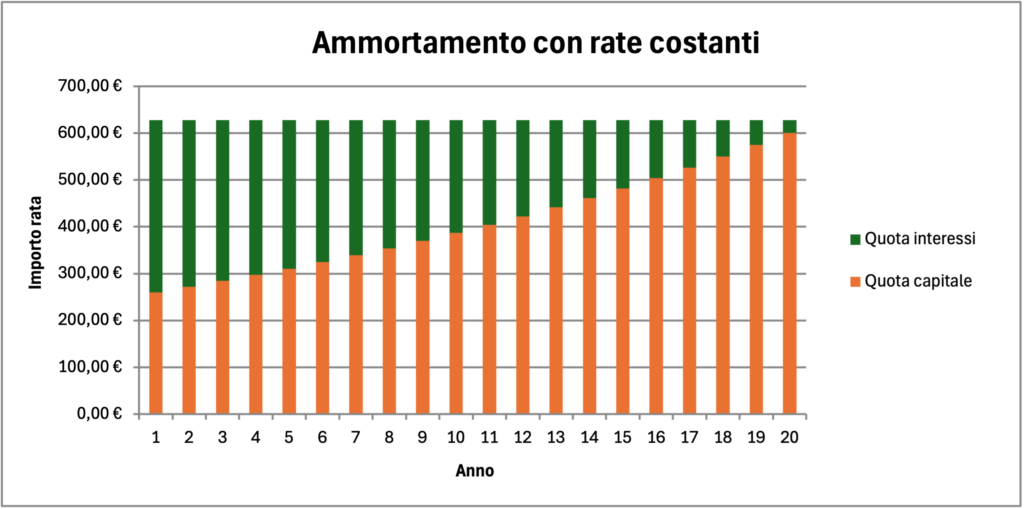
- ammortamento a rata costante o alla francese: l’importo della rata è fisso, ma cambiano, a seconda del periodo, la quota interessi e la quota capitale, con interessi più alti all’inizio;
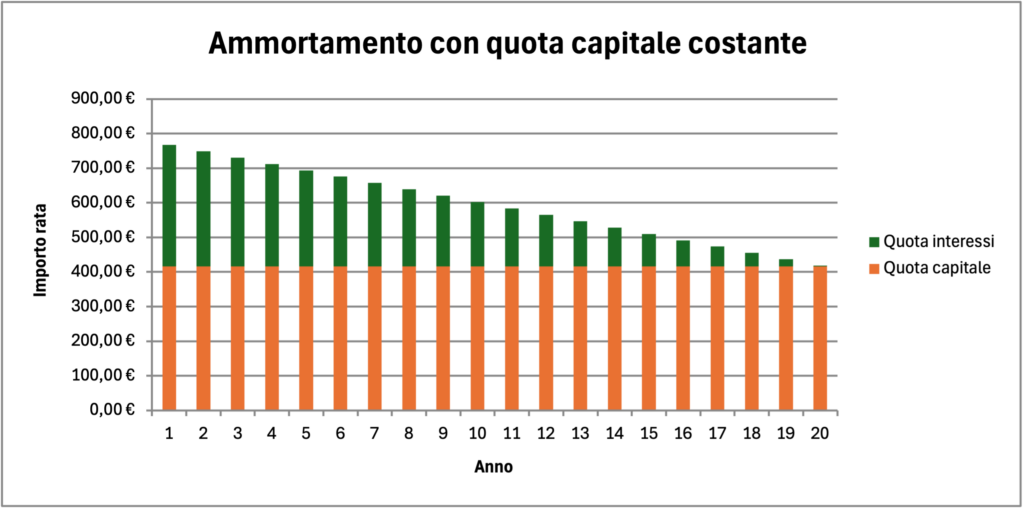
- ammortamento a quota di capitale costante o all’italiana: la quota capitale è la medesima per ciascun periodo, ma la quota interessi varia (decresce) e dunque l’importo della rata è variabile (diminuisce nel tempo);
- ammortamento a due tassi o all’americana: si paga periodicamente la quota interessi, calcolata sull’intero capitale finanziato e distribuita equamente su tutte le rate; la quota capitale, anch’essa costante (e pari al capitale da restituire diviso per il numero di periodi), viene invece versata dal debitore su un fondo e matura un interesse positivo, detto di costituzione (e indipendente dal tasso del finanziamento), in maniera tale che all’estinzione del debito2 l’importo complessivo del fondo coincida con la somma ottenuta in prestito3.
Il passo successivo sarà dunque quello di far esplorare, attraverso l’Intelligenza Artificiale e/o un foglio di calcolo, diversi piani di ammortamento a parità di capitale, periodi e TAEG e far rappresentare l’importo e la composizione della rata per ciascun periodo.
Considerazioni e riflessioni conclusive
Ciascuna delle tipologie di piano descritte presenta vantaggi e svantaggi: la rata costante garantisce un esborso periodico fisso e dunque una più facile pianificazione delle spese, ma comporta un costo complessivo maggiore; viceversa, un piano a rate decrescenti è complessivamente meno oneroso, ma le rate iniziali possono essere meno sostenibili in un bilancio familiare; infine, la convenienza di un piano di ammortamento a due tassi dipende dalla differenza tra il tasso passivo (sul capitale in prestito) e il tasso attivo (sul fondo di accantonamento). Un ulteriore aspetto interessante da considerare e confrontare riguarda il risparmio sugli interessi totali in caso di estinzione anticipata del debito (per esempio a metà della sua durata).
Possiamo stimolare studentesse e studenti ad individuare il piano più adatto a un consumatore rispetto a un altro, per esempio sulla base dell’età o della previsione di evoluzione dello stipendio. Per rendere più significativa la comparazione e anche per consolidare i contenuti discussi, è opportuno chiedere loro di costruire i diversi piani di ammortamento per un caso più realistico, sia in importo che in durata, come per esempio un mutuo ventennale pari a $100000$ euro per l’acquisto di una casa con TAN $3,2\%$ e TAEG $4,5\%$. Nelle figure che seguono sono mostrati l’importo e la composizione della rata rispettivamente per l’ammortamento alla francese e per quello all’italiana.
1 Segnalo che la Banca d’Italia fornisce diversi calcolatori online, tra cui quello della rata (costante), reperibile a questa pagina.
2 Per il creditore, in questo piano di ammortamento, l’estinzione del debito avviene alla fine dell’ultimo periodo e dunque il rimborso del capitale è globale e non periodico.
3 In pratica in questo caso si ha una capitalizzazione negativa sul debito e positiva sul fondo.
