L’attività natalizia di quest’anno sarà incentrata sulla famosa “Scuola guida per renne” che ha sede nel Villaggio di Babbo Natale al Polo Nord.
Il lavoro che vi propongo per la classe è una riflessione sugli assi di simmetria di alcuni cartelli stradali (con la possibilità di crearne di nuovi e divertenti!). Piegheremo alcune copie di un triangolo, verificheremo che è un triangolo equilatero e inviteremo studentesse e studenti a illustrarlo in modo che la figura finale abbia un certo numero di assi di simmetria.
Potete usare questo laboratorio come spunto per parlare di educazione stradale, introducendo varie forme di cartelli stradali e i loro significati.
Iniziamo dunque la nostra storia.
È quasi Natale e al Polo Nord c’è grande fermento perché le renne quest’anno dovranno rinnovare la patente polare, senza la quale non potranno consegnare i regali la notte di Natale.
Oggi si devono concentrare sui cartelli di “pericolo/attenzione” e sicuramente devono essere in grado di riconoscerne i principali. Eccone alcuni esempi:
Ma quest’anno Babbo Natale ha deciso di aggiungere nuovi cartelli perché le renne devono stare attente a schivare velocissimi folletti sui loro slittini, giovani renne che giocano a palle di neve e i folletti che si stanno preparando alle gare di salto con gli sci.
Per questo vanno creati cartelli con le indicazioni relative ai pericoli che si possono incontrare tra le nevi. Come avrai notato, i cartelli di pericolo/attenzione sono triangolari. Costruiamone uno insieme.
Prendi un foglio A$4$ e segui le istruzioni.
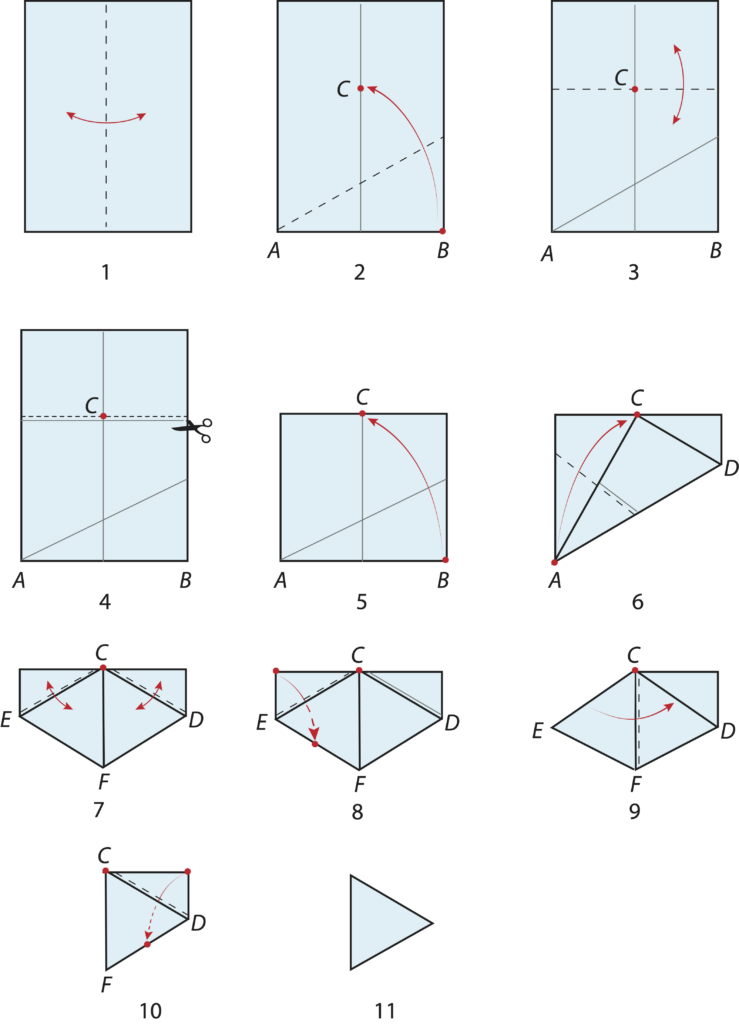
1. Piega e riapri la mediana lunga del rettangolo.
2. Porta il vertice $B$ in basso a destra del rettangolo sulla mediana e piega facendo in modo che la piega passi per il vertice $A$ in basso a sinistra. Segna con un pennarello il punto $C$ dove finisce $B$ e riapri la piega.
3. Esegui una piega parallela ai lati corti del rettangolo, passante per $C$ e riapri. Se vuoi puoi piegare a monte, così vedi bene dove è segnato $C$. Per aiutarti a piegare parallelamente ai lati corti, dovrai portare i lati lunghi su loro stessi.
4. Taglia con le forbici lungo l’ultima piega fatta.
5. Riporta $B$ in $C$ (cioè usa la prima piega fatta).
6. Porta ora $A$ su $C$.
7. La figura che ti appare è suddivisibile in due triangoli centrali, formati da più strati di carta, e due triangoli rettangoli formati da un solo strato di carta. Piega e riapri lungo le ipotenuse $EC$ e $CD$ di tali triangoli (l’ipotenusa corrisponde al lato lungo di questi triangoli e coincide con uno dei lati dei triangoli interni).
8. Considera il triangolo rettangolo a sinistra e piegalo nuovamente lungo $EC$, intascandolo sotto al triangolo centrale a sinistra.
9. Piega ora lungo la linea $CF$.
10. Ripiega lungo $CD$, intascando il triangolo rettangolo.
11. Ecco il triangolo finito.
Divertiti a dimostrare in più modi che il triangolo ottenuto è equilatero e decoralo a piacere per avvisare le renne di prestare attenzione a qualche situazione pericolosa.
In Zona Matematica, nell’area dedicata agli origami, potete trovare una scheda con un’attività completa da proporre per le vacanze di Natale:
Vai all’area “Origami” del I grado
Vai all’area “Origami” del II grado – I biennio