Ripensiamo al significato di media aritmetica!

L’attività didattica che propongo qui è costituita da un problema molto semplice, rielaborazione di un quesito tratto dalle Prove INVALSI 2014 per la classe terza della scuola secondaria di primo grado, che vi consente di far riflettere i vostri alunni sul significato dell’indicatore statistico più semplice e noto, la media aritmetica. Certamente non è difficile ricordare come si calcola la media aritmetica di assegnati valori numerici ma non è sempre scontato afferrarne il ruolo, cioè capire che la media aritmetica si configura come risposta alla richiesta di assegnare lo stesso valore a ciascuno dei dati per conservarne il rispettivo totale: la riflessione sulle differenti strategie possibili richieste nel problema che segue ha proprio questo obiettivo. 

Come ho consigliato altre volte, l’attività può essere assegnata individualmente, tuttavia il mio solito suggerimento è quello di proporla a gruppi o almeno a coppie, perché così l’emergere di strategie differenti risulta facilitata, rendendo poi anche più semplici e partecipi sia la discussione che il confronto fra le soluzioni proposte.

La media degli alunni¹
Una scuola ha dieci classi, con una media di $22$ alunni per classe.
Le classi con $21$ alunni sono sei; le classi con $24$ alunni sono tre.
Quanti alunni ci sono nella decima classe? Descrivete la strategia utilizzata e pensate poi ad una strategia risolutiva diversa.

La richiesta di descrivere la strategia utilizzata non è banale, perché sapete bene che i ragazzi, se non opportunamente abituati all’argomentazione, non solo orale ma anche scritta, trovano difficoltà a esprimere in modo comprensibile il processo di pensiero che ha consentito loro di arrivare a scegliere una procedura. È invece estremamente utile abituarli a questa attività verbale, che consente a tutti un maggior livello di comprensione: più profondo per chi ricorre a una procedura corretta per abitudine, più significativo e più stabile per chi non ha ancora consolidato una modalità corretta di approccio ai problemi.

La richiesta poi di individuare una strategia diversa ha l’obiettivo di indurre i ragazzi a esplorare un modo di pensare differente da quello cui sono ricorsi in prima battuta. Forse penserete che potrebbe bastare che tutti sappiano rispondere alla domanda del problema in almeno un modo, tuttavia la ricerca e l’esistenza di modi differenti per risolvere un problema può contribuire a sollecitare i ragazzi a ricorrere con più fiducia alle loro idee personali: non esistono solo “la regola giusta” o “il procedimento giusto”, ci sono spesso altre vie, che nascono spontaneamente e si rivelano altrettanto opportune. Ecco di seguito come gli alunni potrebbero procedere.

1. La strategia più scolastica può essere quella di calcolare:
   • il numero totale degli allievi della scuola: $22\times10=220$;
   • il numero degli allievi delle $9$ classi: $21\times6+24\times3=126+72=198$
   • e per differenza il numero di quelli della decima classe: $220-198=22$ allievi
     
     
2. Un modo più elementare e costruttivo potrebbe essere suggerito dal fatto che le classi sono solo dieci e di nove di esse è assegnata la numerosità dei rispettivi alunni, schematizzando dunque la situazione così:
   
   $21$ $21$ $21$ $21$ $21$ $21$ $24$ $24$ $24$ ?
   
   Poiché nel testo del problema si afferma che la media degli alunni è $22$, le prime sei classi devono essere completate con un alunno in più ciascuna: i $6$ alunni possono essere esattamente $2+2+2$, prelevati dalle tre classi con $24$ alunni. Risulta evidente a questo punto che la decima classe deve avere esattamente $22$ alunni: qualsiasi altra numerosità farebbe variare la media. Si tratta di una soluzione molto semplice ma richiede che il significato di media aritmetica sia ben padroneggiato e il confronto con la prima strategia proposta potrebbe favorire ulteriormente la comprensione.
   
   
3. Un’altra strategia, collegabile a quella elementare, potrebbe essere quella di ricorrere ad una rappresentazione grafica, che rende ancora più evidente il procedimento costruttivo descritto al punto precedente. Per esempio usando un grafico come quello riportato sotto, distribuendo i “pezzi” di rettangoli che superano la media (rappresentata dalla linea nera) in modo che siano “aggiunti” alle classi che non la superano, si osserva che tutte le nove classi arrivano esattamente alla linea nera corrispondente alla media, quindi la decima classe deve avere un numero di studenti uguale alla media, cioè $22$ alunni.

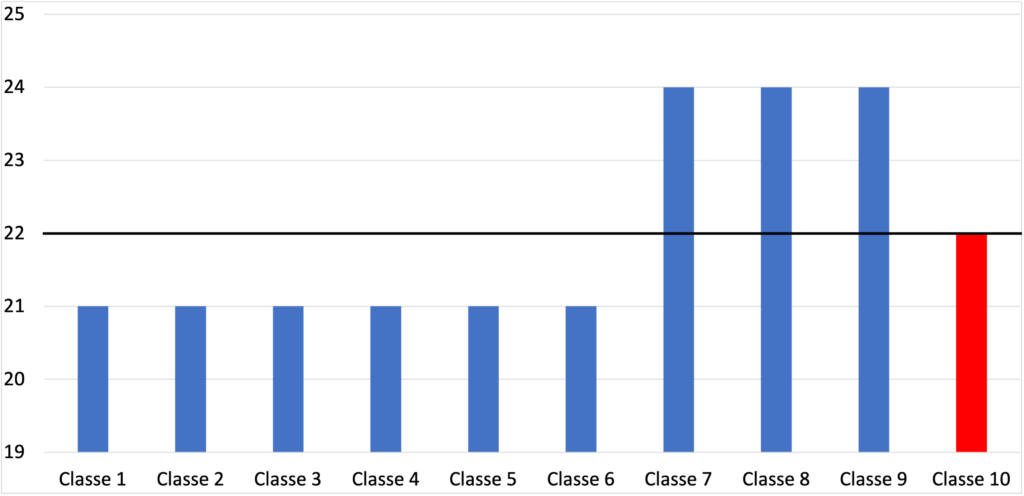
Dalle soluzioni  proposte è evidente che pur essendo semplice l’aritmetica cui occorre riferirsi, ciò che è importante ricostruire (o comunque rivedere) è il significato di media aritmetica. 

Scopo di questa proposta vuole proprio essere quello di rafforzarne il significato, mettendo in secondo piano l’aspetto del calcolo. Riflettere sul significato di media aritmetica, interpretandolo su esempi anziché ripassandolo mnemonicamente, è un lavoro decisamente più utile e fruttuoso, che favorisce negli studenti l’interiorizzazione del concetto.

Un possibile sviluppo di questo problema potrebbe essere quello di proporre la stessa situazione con due dati mancanti, aggiungendo per esempio il quesito:

Se le classi con $21$ alunni fossero solo cinque, quanti alunni potrebbero esserci nella nona e nella decima classe? (Considerate che il numero minimo di alunni per formare una classe è $16$).

Ripercorrendo una delle strategie proposte, si arriva a scoprire che si tratta di suddividere in due classi $43$ alunni e questa volta dunque la soluzione non è unica, sono possibili infatti le composizioni seguenti (tenendo conto che il minimo di alunni per classe è $16$): $16$ e $27$; $17$ e $26$; $18$ e $25$; $19$ e $24$; $20$ e $23$; $21$ e $22$.

La molteplicità di soluzioni, come sapete, non è abituale nelle situazioni problematiche che si propongono ai ragazzi ma risulta sempre molto interessante e nel nostro caso illustra ancora meglio come a parità di media aritmetica siano possibili situazioni differenti, tutte comunque leggibili dallo stesso dato di sintesi, la media aritmetica: anche questo aspetto ne favorisce dunque una sua più consapevole interiorizzazione.

^{1 Item D15, INVALSI 2014 per la terza classe della scuola secondaria di I grado. Nel quesito originale alla domanda seguivano quattro possibili risposte (A. $20$; B. $22$; C. $23$; D. $25$) e mancava la richiesta di argomentazione sulla strategia risolutiva.}