
Per iniziare al meglio il nuovo anno scolastico possiamo creare un quadro di cornici che contengano un ricordo delle vacanze oppure un augurio, un suggerimento o un buon proposito per il nuovo anno scolastico.

Ovviamente ne approfittiamo per proporre un’attività matematica: lavoriamo sui quadrati e le loro aree.
A ogni studentessa e a ogni studente occorreranno $3$ fogli di carta origami quadrata di lato $15$ cm, bianco su una faccia e colorato sull’altra. Le istruzioni che seguono vanno ripetute per due fogli fino al passaggio $4$ e per il terzo foglio fino all’ultimo passaggio.
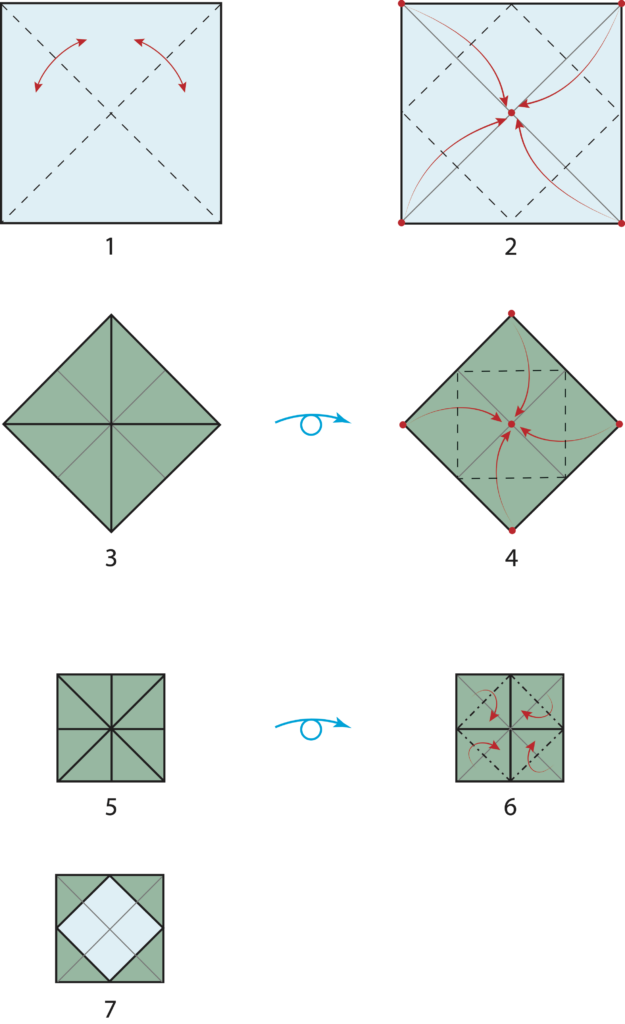
Istruzioni di piegatura:
1. Bianco sopra. Piega e riapri le due diagonali.
2. Porta i quattro vertici nel centro del quadrato.
3. Ecco la figura che ottieni dopo il passaggio 2. Ora volta la frittata.
4. Porta i quattro vertici al centro.
5. Ecco la figura che ottieni dopo il passaggio 4. Ora volta la frittata.
6. Il quadrato più grande è diviso in 4 quadrati più piccoli. Piega a monte lungo le diagonali dei quadrati piccoli indicate, nascondendo metà di ogni quadrato sotto la restante metà. Per facilitare la mossa, puoi prima piegare a valle e poi ribaltare la piega.
7. Ecco la cornice completata.
Con i fogli piegati fino al passaggio finale si ottengono le cornici che possono poi essere incollate su un cartellone, una vicina all’altra, con all’interno il ricordo/augurio scelto, come mostra la foto iniziale.
Gli altri due fogli, una volta riaperti, presenteranno questo crease pattern (traccia lasciata dalle pieghe):
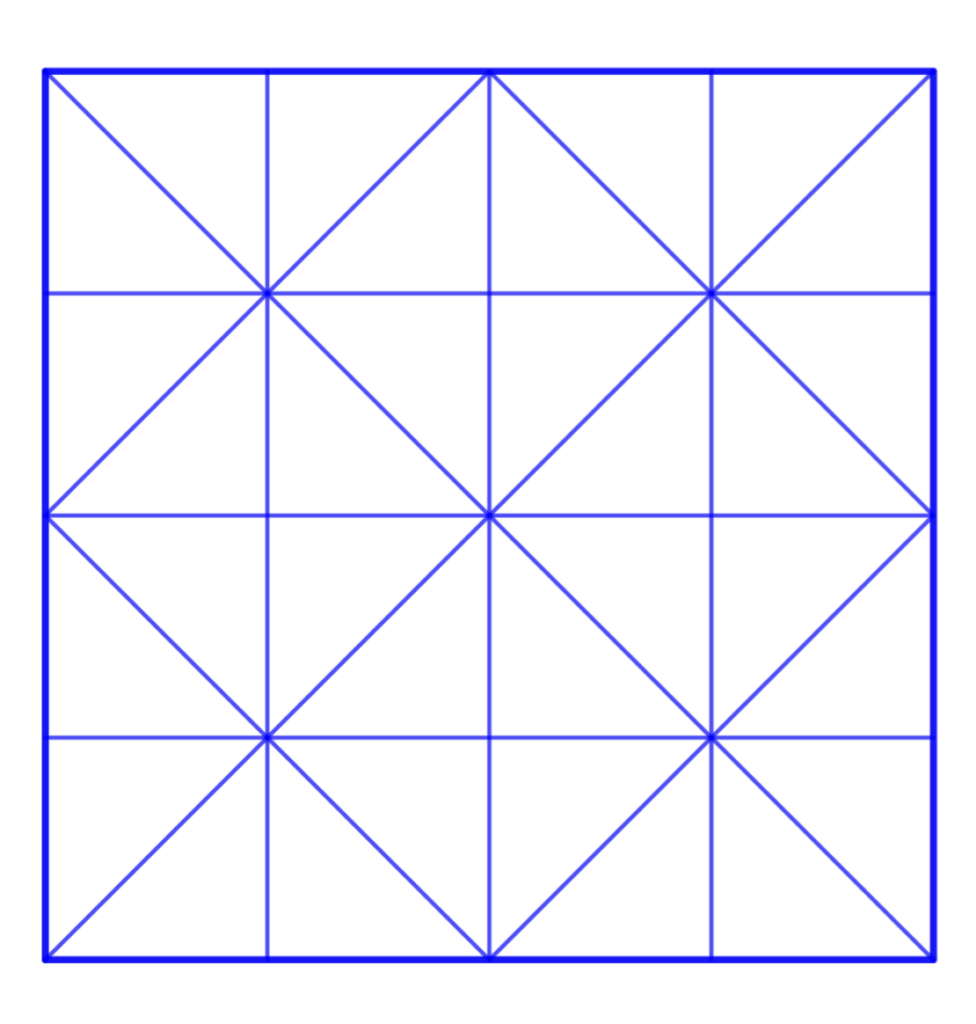
Possiamo far colorare i quadrati in esso contenuti, osservando la presenza di due “famiglie” di quadrati: quella nella quale i lati sono paralleli a quelli del quadrato di partenza e quella nella quale i lati sono paralleli alle diagonali del quadrato di partenza.
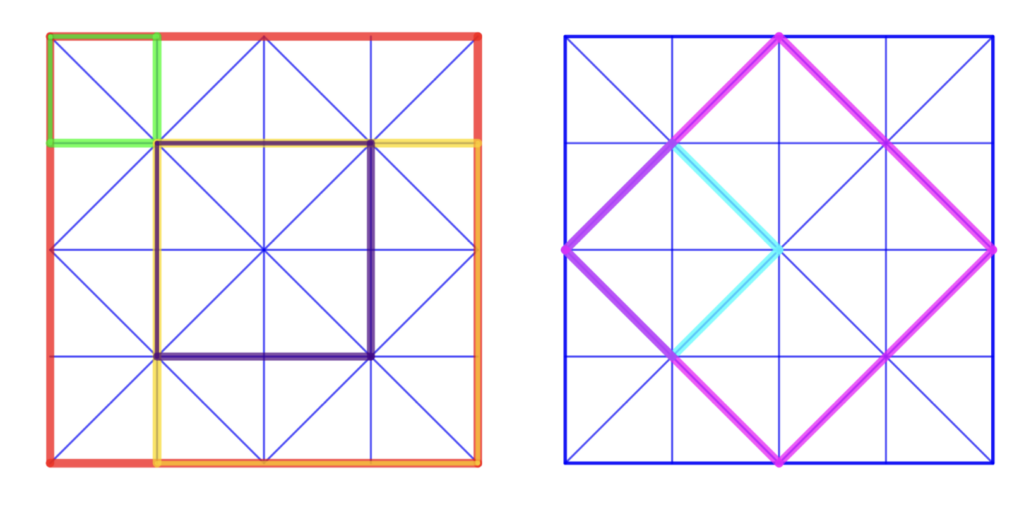
Lavorando sulle famiglie separatamente o ampliando il confronto ai quadrati di entrambe le famiglie, si potrà chiedere la relazione tra lati, perimetri e aree dei vari quadrati. Relativamente al confronto tra i lati di tutti i quadrati che compaiono, osserviamo che per un calcolo quantitativo occorre conoscere $\sqrt{2}$; il confronto tra aree non necessita invece di questa informazione.
In Zona Matematica, nell’area dedicata agli origami, potete trovare una scheda da proporre alla classe e relative soluzioni.
Vai all’area “Origami” del I grado
Vai all’area “Origami” del II grado – I biennio
