
Per iniziare il $2026$ si potrebbe proporre un’attività che spesso coinvolge favorevolmente studentesse e studenti e li stimola a costruire un semplice modello matematico rappresentato da un’equazione di secondo grado, modello versatile per le varie classi e per i vari livelli di competenza raggiunti, che offre un grado di complessità regolabile.
All’interno dei campi da basket e da pallavolo sia dei centri sportivi che delle scuole sono segnate delle linee distanziate fra loro che vengono utilizzate da mister e docenti di Educazione motoria per una particolare attività di sprint: ragazze e ragazzi devono correre velocemente per toccare ogni linea tornando ogni volta al punto di partenza prima di andare a toccare la linea successiva. La prova si considera completata quando sono state toccate tutte le linee per poi tornare al punto di partenza.
Per consentire alla nostra classe di costruire un semplice modello matematico che calcoli i metri effettuati per completare ogni attività, semplifichiamo la situazione reale stabilendo la distanza della prima linea a $3$ metri dalla partenza e quella fra ogni linea e la successiva di $1$ metro. Invitiamoli a schematizzare la situazione:
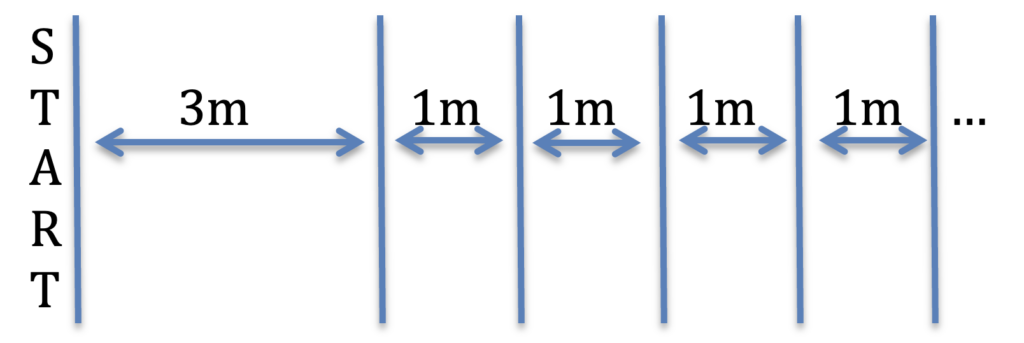
Inizialmente calcoliamo solo i metri $m_{n}$ per arrivare a toccare l’ultima linea (l’$n$-esima).
Per determinare in modo semplice i metri da percorrere per toccare $n$ linee occorre trovare una relazione diretta fra $m_{n}$ ed $n$. Il modo più semplice è considerarla come somma di due espressioni:
- la prima corrisponde ai metri percorsi solo per ripetere la distanza dallo Start alla prima linea ($3$ metri nel nostro caso, ripetuti per $2n$ volte, meno i $3$ metri per ritornare allo Start – abbiamo deciso di conteggiare inizialmente solo i metri percorsi per arrivare a toccare la linea):
$3\left( 2n-1\right)$
- la seconda corrisponde ai metri percorsi ripetutamente dalla prima linea alla linea $n$-esima: $1$ metro dalla prima alla seconda linea (avanti e indietro), $2$ metri dalla prima alla terza e cosi via:
$1+1+2+2+…+\left( n-3\right)+\left( n-3\right) +\left( n-2\right) +\left( n-2\right)+\left( n-1\right)$
che, addizionando il primo termine con il penultimo, il secondo con il terzultimo ecc., risulta un’addizione ripetuta di $\left( n-1\right)$ metri per $\left( n-1\right)$ volte:
$\left[ 1+\left( n-2\right) \right]+\left[ 1+\left( n-2\right) \right] +…+\left( n-1\right)=\left( n-1\right) ^{2}$
La relazione è molto semplice ed esprimibile tramite un polinomio di secondo grado.
Proseguendo per tentativi ponderati, verifiche, riflessione sugli eventuali errori e messa in atto di ulteriori prove, alla portata di studentesse e studenti, la relazione che modellizza la situazione si scopre essere:
$m_{n}=3\left( 2n-1\right) +\left( n-1\right) ^{2}$ ossia $m_{n}=n ^{2}+4n-2$
L’estensione al caso di una generica distanza $s$ della prima linea dallo Start non comporta poi particolari difficoltà:
$m_{n}=s\left( 2n-1\right)+\left( n-1\right) ^{2}$ ossia $m_{n}=n^{2}-2\left(1-s\right)n+1-s$
Per completezza di rappresentazione della vera attività di Scienze motorie, è bene studiare anche il caso del calcolo dei metri da percorrere per tornare allo Start dopo aver toccato l’ultima linea.
Occorre semplicemente aggiungere alla relazione i metri da percorre per ritornare allo Start dall’ennesima linea, $n-1+s$, da cui
$m_{n}=n^{2}-2\left( 1-s\right)n+n$ ossia $m_{n}=n^{2}-n\left( 1+2s\right)$
Per le studentesse e gli studenti con competenze avanzate o per gli ultimi anni della scuola secondaria di secondo grado si può chiedere di generalizzare il modello per qualsiasi distanza $s$ della prima linea dallo Start e distanza $d$ fra ogni linea e la successiva. Altrimenti si guiderà comunque la classe a scoprire che lo schema rappresentativo diventa:
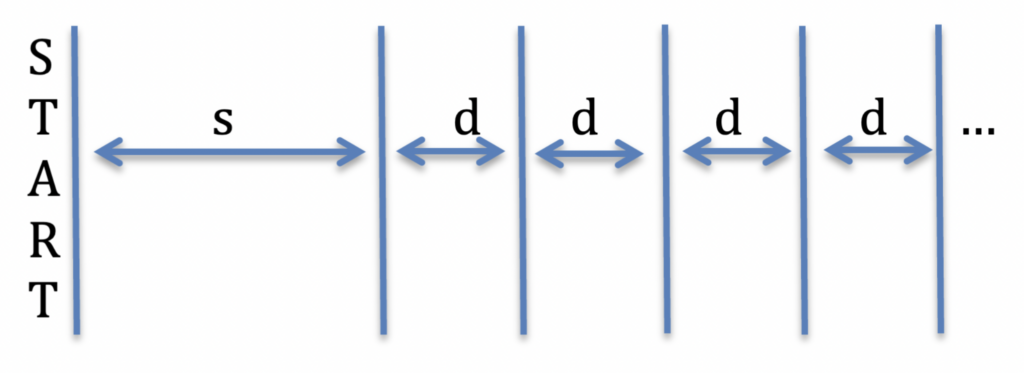
e la relazione matematica di modellizzazione si trasforma in:
$m_{n}=2ns+dn\left( n-1\right) $
Di norma le linee predisposte sono $4$ e le misure più verosimili di $s$ e $d$ potrebbero essere, ponendo $n=4$, $s=2,00$ m, $d=2,21$m:
$m_{4}=8\left( 2,00\right)$ m $+12\left( 2,21\right)$ m=$16$ m $+26,52$ m $=40,52$ m
Studentesse e studenti generalmente ripetono lo sprint almeno $2$ volte per ogni lezione e, supponendo che le lezioni in cui viene svolto l’esercizio durante l’anno siano circa $25$, i metri $M$ percorsi nel $2026$ saranno proprio:
$M_{2026}=25\cdot 2m_{4}=25\cdot 2\cdot40,52=2026$ m
Non resta che augurare buon $2026$!
