
A conclusione di questo ciclo di articoli sull’applicazione della Matematica all’educazione civica, vi propongo un’attività di analisi relativa ad alcuni dati sulla dispersione scolastica. L’istruzione, infatti, è un settore strategico per ciascun Paese, in quanto strumento di promozione sociale e benessere economico, ed è espressamente tra gli obiettivi indicati dall’Agenda $2030$ delle Nazioni Unite. Negli ultimi anni, la scuola ha risentito in maniera significativa delle conseguenze, più o meno dirette, della pandemia da Covid-$19$: in Italia la didattica a distanza ha sostituito o affiancato, anche per periodi lunghi, la tradizionale attività in presenza, con una riduzione dell’efficacia degli apprendimenti (nonostante gli sforzi messi in campo da docenti e famiglie), in particolare per gli alunni più svantaggiati. A ciò si è aggiunto un crescente disagio psicologico degli allievi, privati della fondamentale dimensione relazionale del rapporto educativo1.
Secondo l’analisi dell’Istituto INVALSI, uno degli effetti collaterali della situazione pandemica è stato l’aggravarsi della dispersione scolastica, in particolar modo della sua componente implicita, che si traduce nella mancata acquisizione delle competenze essenziali da parte di molti studenti che pure completano il ciclo di istruzione e conseguono il relativo diploma. Seppure più complessa da quantificare rispetto a quella esplicita2, la dispersione implicita emerge dai risultati delle prove di Italiano, Matematica e Inglese predisposte dall’Istituto e somministrate a conclusione del ciclo di istruzione secondaria di secondo grado a tutti gli studenti.
L’attività che vi propongo è focalizzata appunto su un’analisi quantitativa del fenomeno e può essere utilizzata per introdurre il concetto di coefficiente angolare di una retta.
Parte A
1. Definizione di dispersione scolastica esplicita: la situazione italiana e quella europea
Iniziamo questa attività spiegando che cosa si intende per dispersione scolastica esplicita: essa rappresenta la percentuale di giovani nella fascia di età tra i $18$ e i $24$ anni che non hanno conseguito un titolo di istruzione secondaria e non sono più in formazione (Early Leavers From Education and Training). I dati ufficiali sulla dispersione scolastica sono forniti, su base annua, dall’Istat e, a livello europeo, dall’Eurostat e consentono di avere un’idea dell’efficacia delle misure adottate da ciascun Paese ai fini del raggiungimento del comune obiettivo di ridurre il fenomeno, entro il $2030$, al di sotto del $9\%$.
Il primo spunto di riflessione per i ragazzi può essere costituito dai seguenti dati che forniscono le dimensioni del fenomeno in Italia e in Europa.
In tabella è riportata la percentuale di giovani dai $18$ ai $24$ anni di età che abbandonano prematuramente gli studi (fonte dei dati: Istat).
| Anno $2008$ | Anno $2008$ | Anno $2008$ | Anno $2020$ | Anno $2020$ | Anno $2020$ | |
| Maschi | Femmine | Totale | Maschi | Femmine | Totale | |
| Nord-Ovest | $21,8$ | $15,3$ | $18,6$ | $14,1$ | $9,3$ | $11,8$ |
| Nord-Est | $18,9$ | $12,6$ | $15,8$ | $11,6$ | $8,1$ | $9,9$ |
| Centro | $16,6$ | $11,9$ | $14,3$ | $14,4$ | $8,4$ | $11,5$ |
| Sud | $26,4$ | $20,9$ | $23,7$ | $19,1$ | $13,2$ | $16,3$ |
| Italia | $22,4$ | $16,7$ | $19,6$ | $15,6$ | $10,4$ | $13,1$ |
Nell’istogramma in figura è riportata la percentuale di ELET in Europa (fonte dei dati: Eurostat, anno di riferimento: $2020$).
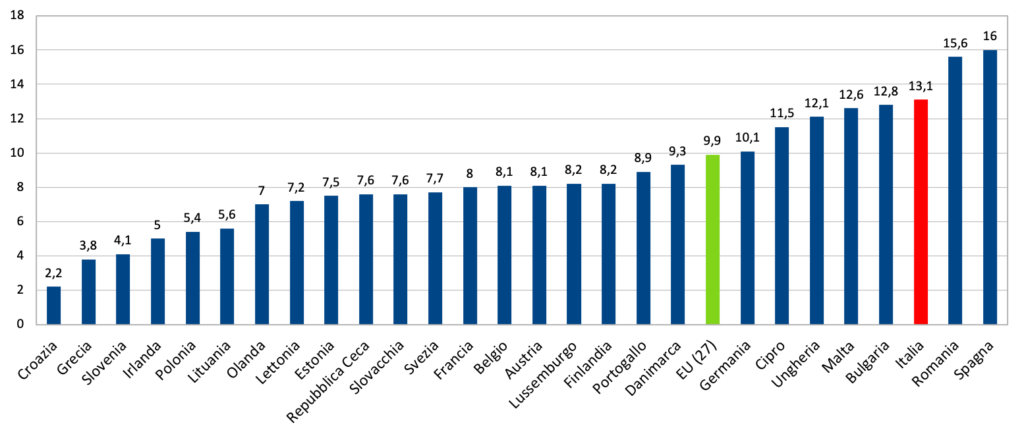
Sulla base dei dati in tabella possiamo chiedere ai ragazzi di rappresentare l’andamento temporale della dispersione esplicita per le varie macroaree geografiche e, separatamente, per maschi e femmine.
2. Effetti della dispersione esplicita
Sottoponiamo ai ragazzi la figura $3.21$ del rapporto annuale dell’Istat per il $2021$: quanto è difficile per un ELET entrare nel mondo del lavoro? Iniziamo chiedendo ai ragazzi, tramite una ricerca mirata sul sito dell’Istat, di confrontare il tasso di occupazione degli ELET con quello dei giovani nella stessa fascia d’età che hanno completato il percorso formativo.
Successivamente possiamo invitarli a tradurre le informazioni presenti nel diagramma a barre in un grafico a dispersione che mostri, per ciascuna area geografica, l’evoluzione nel tempo. Che tipo di trend si osserva nel periodo considerato ($2008$-$2020$)? Se ci limitassimo a rappresentare la situazione all’inizio e alla fine, come potremmo confrontare quantitativamente la “rapidità” con cui si è ridotto, mediamente, il numero di occupati in un’area geografica piuttosto che in un’altra? Queste considerazioni dovrebbero portare al concetto di pendenza di una retta, da cui si potrebbe quindi passare alla definizione formale di coefficiente angolare. Successivamente si potrebbe allargare la discussione a una rappresentazione che contenga i valori disponibili per tutti e quattro gli anni, per introdurre la discussione sulle funzioni lineari a tratti.
Parte B
3. La dispersione implicita: confronto tra i livelli pre e post-pandemici
La definizione di dispersione implicita è stata recentemente introdotta dall’Istituto INVALSI e quantificata attraverso il numero di giovani che hanno raggiunto al massimo il livello $2$ in Italiano e Matematica3 e che non hanno raggiunto neppure il livello B$1$ in Inglese sia per la prova di lettura che per quella di ascolto (ricordiamo che, secondo l’ordinamento italiano, al termine del ciclo di istruzione secondario gli studenti dovrebbero raggiungere il livello B$2$).
Sul sito dell’Istituto è disponibile un’interessante serie di dati che confrontano i risultati delle prove somministrate agli studenti dell’ultimo anno della scuola superiore di secondo grado negli anni $2019$ e $2021$. In particolare, viene mostrata la dispersione implicita pre e post-pandemia sia a livello nazionale che per singola regione. Possiamo quindi sottoporre ai ragazzi le serie temporali del $2019$ e $2020$ e chiedere loro, come esercizio, di determinare il coefficiente angolare dei segmenti rappresentati, dopo aver spiegato come calcolarlo dalle coordinate di due punti. È utile stimolarli a riflettere sul significato del segno di tale parametro e/o sull’implicazione di un coefficiente angolare nullo. Un esercizio interessante può essere quello di estrapolare il punto relativo al $2022$, se l’andamento riscontrato dovesse essere confermato (è probabile che nei prossimi mesi l’INVALSI pubblichi i dati relativi al $2022$).
È infine possibile ampliare l’analisi sulla propria regione e per area disciplinare (basta selezionare la regione di interesse ed esplorare i risultati pubblicati per materia e per grado) in modo da avere un’idea di quali siano le competenze più deficitarie e/o siano state maggiormente compromesse negli ultimi anni.
4. Confronto con la dispersione esplicita e calcolo della dispersione totale
A conclusione dell’attività, possiamo chiedere ai ragazzi di stabilire:
a. se nel periodo $2019$-$2021$ è stata più significativa la variazione della dispersione esplicita o di quella implicita;
b. in che misura ciascuna di esse contribuisce alla dispersione totale, a livello nazionale e a livello regionale;
c. quanto è realistico per il nostro Paese il raggiungimento dell’obiettivo fissato ($9\%$) entro il $2030$ e quale dovrebbe essere, a tale scopo, il tasso di riduzione annuo del fenomeno.
1 https://www.ilsole24ore.com/art/censis-depressione-e-disagi-gli-effetti-pandemia-studenti-AEEDV10, https://www.senato.it/application/xmanager/projects/leg18/attachments/documento_evento_procedura_commissione/files/000/263/201/Consiglio_nazionale_ordine_psicologi.pdf, https://www.senato.it/service/PDF/PDFServer/DF/367468.pdf
2 Per dispersione esplicita si intende la percentuale di ragazze e ragazzi che abbandonano precocemente gli studi o i percorsi di formazione professionale, senza pertanto conseguire il diploma o i necessari attestati. La dispersione esplicita è misurata dall’Istat, che censisce e riporta annualmente la percentuale di giovani tra i $18$ e i $24$ anni che hanno conseguito al più il diploma di secondo grado inferiore (licenza media) e che non possiedono qualifiche professionali almeno biennali o non frequentano né corsi scolastici né attività formative.
3 I livelli di competenza sono indicati attraverso un punteggio che va da $1$ (non adeguato) a $5$ (molto buono) per Italiano e Matematica e in base al QCER-Quadro Comune Europeo di Riferimento per la conoscenza delle lingue nelle prove di Inglese (da A$1$ a C$2$).
