
A volte capita di leggere sui social media frasi attribuite ad autori famosi, anche se molto spesso non è così: Bukowski e Einstein, in questo senso, vanno per la maggiore.
Ultimamente mi è accaduto più volte di leggere una frase attribuita a Aldous Huxley, anche se, a quanto pare, non si trova scritta in nessuna delle sue opere, per cui resta il dubbio sulla sua effettiva provenienza.
La frase però mi ha fatto riflettere, perché mette in evidenza, se ce ne fosse stato il bisogno, la dicotomia tra ciò che si dovrebbe fare e il mondo reale. E io avverto questa dicotomia sia come insegnante, per me e per solidarietà con tutte le mie colleghe e tutti i miei colleghi, sia come autore, per lo stesso motivo.
La frase recita:
“Ci sono tre tipi di intelligenza: l’intelligenza umana, l’intelligenza animale e l’intelligenza militare”.
Prometto che leggerò le opere di Huxley – a suo tempo mi sono fermato a Orwell e Bradbury – ma mi è venuto spontaneo, a questo proposito, chiedermi quale di questi tre tipi di intelligenza educhiamo quando insegniamo matematica.
Tra l’altro la mia domanda è legata a una serie di considerazioni che si stanno facendo in ambiti accademici e ministeriali – in realtà è da molti anni, anche se con un successo piuttosto limitato – sull’insegnamento della matematica troppo arido, poco accattivante, solamente addestrativo eccetera. Ne parlano in questo periodo ministri, premi Nobel e chi più ne ha più ne metta.
Il succo è che i nostri studenti sono bravi a fare calcoli – quelli che sono bravi, si intende – ma non sono bravi a risolvere problemi e quelli che non sono bravi a fare calcoli generalmente si perdono per strada, perché pensano che la matematica sia solo un insieme di regole che non servono a niente.
Mi verrebbe da dire che sviluppiamo in alcuni l’intelligenza militare e basta, quella di tipo esecutivo, finalizzato al calcolo. Di fronte a una richiesta del tipo “A che cosa serve questa formula?”, la tentazione a volte è di rispondere, più o meno implicitamente, ”Non devi preoccuparti: è così, tu usala come ti ho detto e basta”.
Ci sarebbe poi l’intelligenza animale, finalizzata perlomeno a procurarsi di che vivere: lì la matematica potrebbe servire pure a qualcosa – e non solo a chi porta a casa uno stipendio grazie a essa – ma sembra che la maggior parte delle persone abbia come unico ricordo di ciò che ha appreso a scuola le proporzioni che, peraltro, spesso usa a sproposito.
E l’intelligenza umana? Credo sia quella della fantasia, della creatività, della logica, dell’arte, dello sport, della socialità. Non vediamo, da insegnanti ed educatori, il legame che la “nostra” matematica ha con tutti questi aspetti del sapere e dell’umanità?
Non si tratta di costruire specchietti per allodole solo per catturare l’attenzione, ma di dare significato alle idee, magari anche partendo da un gioco, ma non fine a sé stesso. Guardare un concetto da più angolazioni, esprimerlo con registri diversi e saltare da uno all’altro, visualizzare.
Faccio un esempio. Qualche anno fa ai Giochi di Archimede è comparso questo quesito:
Indicare la più grande tra queste frazioni.
(A) $\dfrac{2018}{2011}$ (B) $\dfrac{2016}{2009}$ (C) $\dfrac{2020}{2013}$ (D) $\dfrac{2019}{2012}$ (E) $\dfrac{2025}{2018}$
Non ho idea di quale sia stata la percentuale di risposte giuste, sbagliate, non date. Preferisco vedere che cosa c’è sotto.
Il militare che c’è in me (no eh!) mi suggerisce “Facciamo il denominatore comune e confrontiamo i numeratori”, però poi interviene subito l’animale a fermarlo: “Ma chi te lo fa fare? Prendi la calcolatrice e fai le divisioni, no?”.
Proviamo a essere un po’ più umani? C’è una regolarità in quelle frazioni. Se chiamiamo $x$ il denominatore variabile, il numeratore è sempre $x+7$: allora c’è l’algebra, che non serve solo a fare i prodotti notevoli; c’è una frazione, che possiamo scrivere $\dfrac{x+7}{x}$, ma anche $1+\dfrac{7}{x}$. Allora qualcosa comincia a vedersi, perché è tutto costante, tranne $x$ che varia: e più diventa grande, più la nostra frazione diventa piccola (e, tra l’altro, tutto questo non ha nulla a che fare con le proporzioni!).
Ma c’è pure una funzione, che possiamo scrivere $f\left( x\right) =1+\dfrac{7}{x}$ e ha un grafico fatto più o meno così:
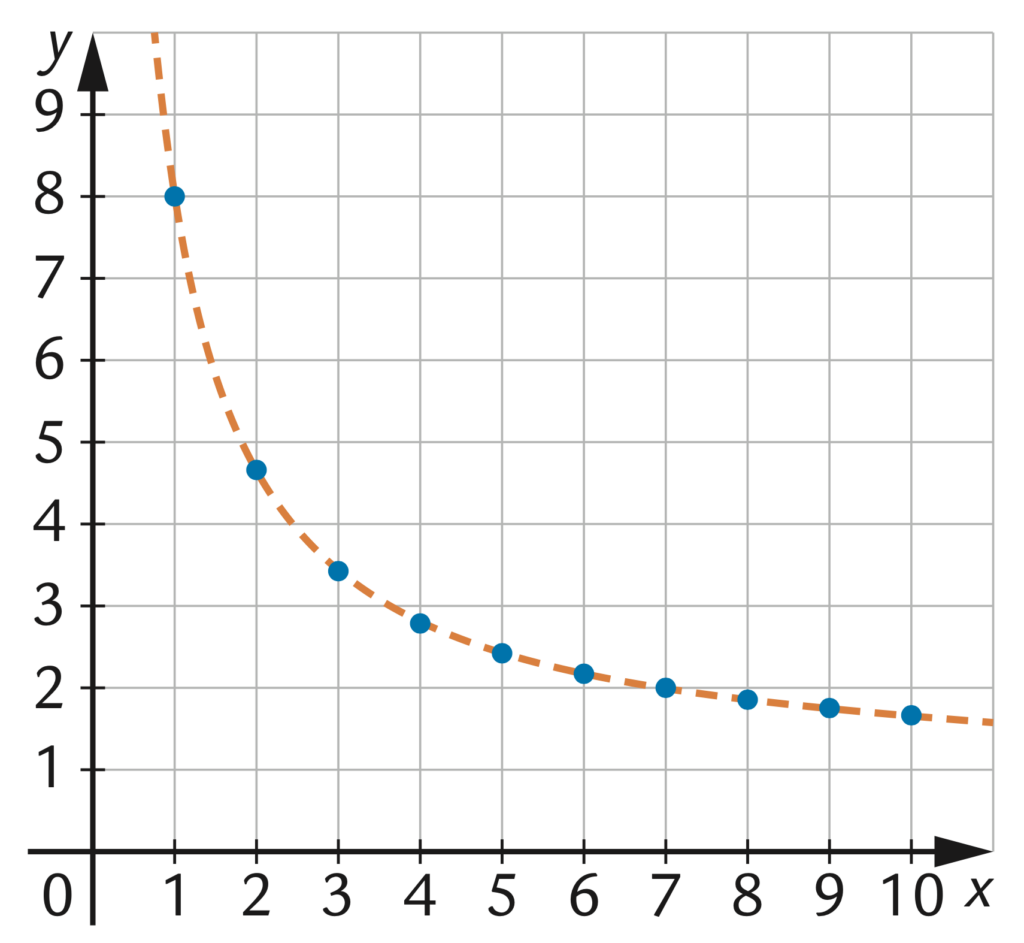
E qui si vede tutto benissimo: visualizzare…
Che curva è quella tratteggiata? Lo sappiamo: è un’iperbole. Anzi, magari possiamo partire da questo giochino per introdurla, oppure per parlare di funzioni, oppure quello che volete.
Il gioco non è più soltanto un gioco: abbiamo messo insieme tanti aspetti diversi, saltando da un registro all’altro. E forse abbiamo capito qualcosa in più.
Magari adesso possiamo anche tentare una dimostrazione rigorosa; può darsi che riescano a fare i conti anche le ragazze e i ragazzi meno bravi e comprendano come si usano i principi di equivalenza delle disuguaglianze: partiamo da $x_{1} <x_{2}$ e arriviamo a $1+\dfrac{7}{x_{2}} <1+\dfrac{7}{x_{1}}$.
E tutto questo può essere fatto in un contesto di laboratorio: attenzione che parlo di contesto e non di stanza fisica. Possiamo usare strumenti che ci aiutino nell’esplorazione: fogli di calcolo, software.
Ecco: in questo anno scolastico che si apre con buoni propositi di matematiche più accattivanti e intelligenze militari spopolanti, il mio augurio è quello di trovare una strada ricca di significati “umani”.
