
Molto spesso negli articoli di giornale che si occupano di salute leggiamo notizie di questo tipo:
Una ricerca ha scoperto una correlazione tra l’alimentazione e la salute del cuore. Secondo gli scienziati maggiore è la quantità di frutta consumata, minore è la probabilità di avere un infarto.
Posto che l’esempio è inventato, articoli di questo tipo potrebbero indurci a pensare che ci sia un rapporto di causa-effetto tra le due variabili di cui si parla (la quantità di frutta e la probabilità di infarto) per cui cambiando la nostra alimentazione potremmo ottenere dei benefici di salute.
Questa conclusione, tuttavia, non è sempre vera. Esistono casi in cui delle grandezze presentano una correlazione statistica ma non hanno alcun rapporto di causa-effetto che le colleghi.
Cerchiamo di capirne il motivo ripassando brevemente il concetto di correlazione.
A partire da un’analisi statistica che coinvolga due variabili quantitative $X$ e $Y$, si può calcolare l’indice di correlazione lineare tra le due variabili. Si tratta di un numero compreso tra $-1$ e $+1$ che descrive quanto l’insieme delle coppie di valori tende a distribuirsi lungo una linea retta. Nei casi estremi in cui l’indice è uguale a $+1$ o $-1$ le due variabili si trovano esattamente su una linea retta, nel primo caso con coefficiente angolare positivo, nel secondo caso con coefficiente angolare negativo.
Nelle seguenti immagini vediamo cinque esempi nei quali le variabili hanno correlazione rispettivamente uguale a $0$, $0.5$, $0.8$, $0.9$, $0.99$.
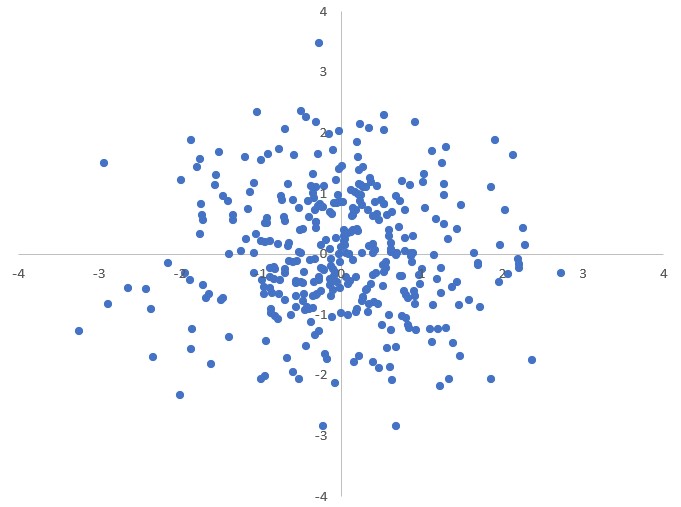
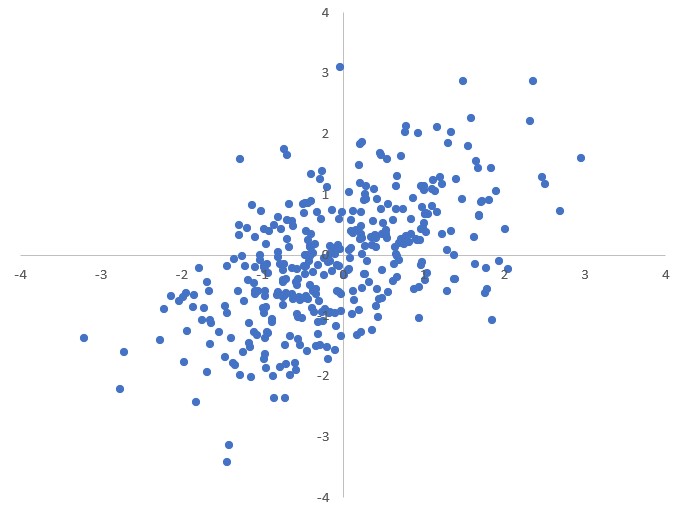
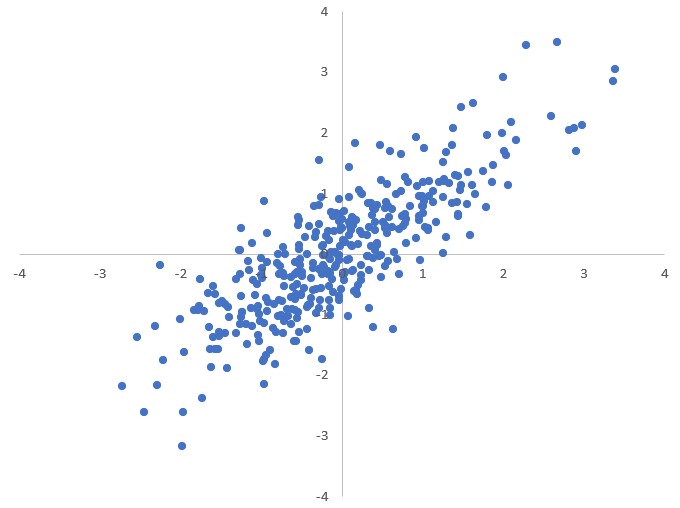
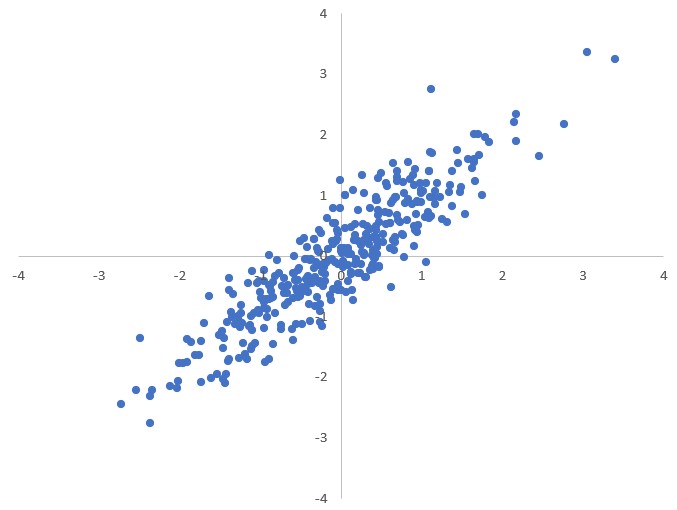
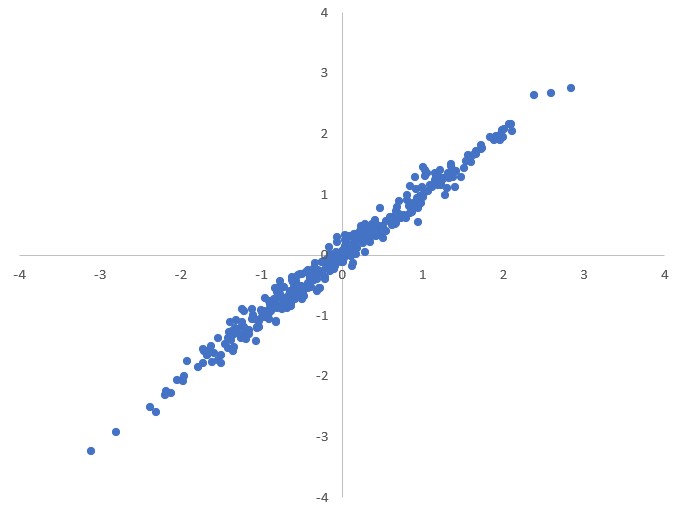
L’indice di correlazione descrive il modo in cui si distribuiscono le due variabili una rispetto all’altra ma non può essere una prova che esse siano legate da un rapporto di causa-effetto.
Vediamo un esempio per chiarire la questione.
Per un intero anno in una località di mare si contano ogni giorno il numero di multe che vengono notificate e il numero di gelati venduti.
Viene creato un grafico con i dati ottenuti che risulta essere il seguente:
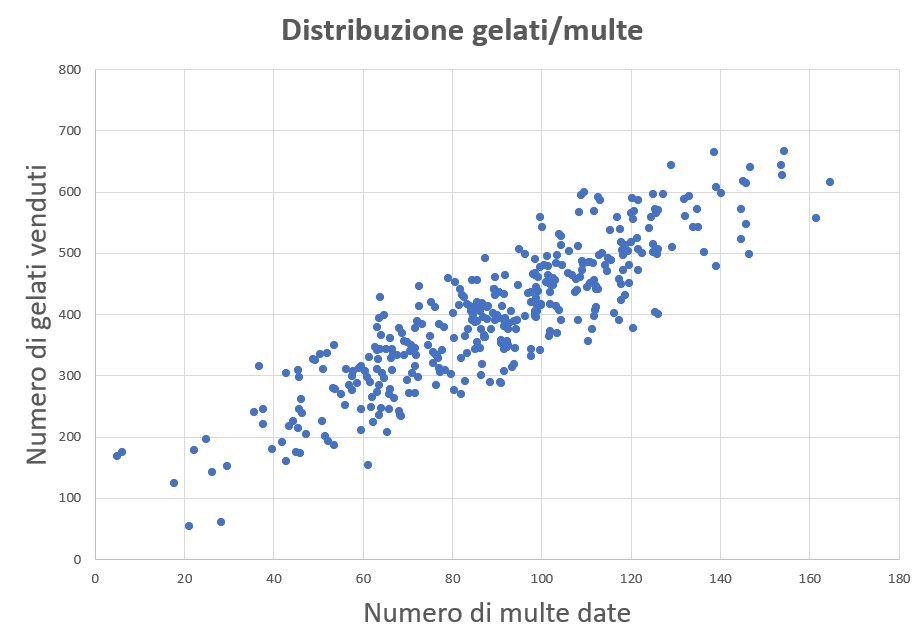
Se si calcola la correlazione tra le due variabili si ottiene un valore di $0.9$.
Dal grafico e dal valore ottenuto risulta evidente che tra le due variabili vi sia una correlazione molto alta, eppure tra loro non esiste alcun rapporto di causa-effetto: comprare un gelato non vi farà prendere una multa e prendere una multa non vi costringerà a comprare un gelato (anche se quest’ultimo potrebbe essere fonte di consolazione).
Entrambe le variabili sono strettamente legate a un altro elemento: il numero di persone che si recano alla località di mare. Nei giorni in cui la località è più frequentata si venderanno più gelati e verranno notificate più multe. Viceversa, quando nella località sono presenti poche persone allora queste due variabili avranno entrambe valori più bassi.
Ecco, quindi, che cosa può succedere: le due variabili possono dipendere entrambe da una causa comune, ma non aver alcun rapporto di causa-effetto tra loro.
Nelle analisi mediche è molto difficile separare i veri fattori che portano a dei benefici da quelli che sono invece correlati a un migliore stato di salute solo per motivi statistici.
Mangiare molta frutta potrebbe essere correlato a una minore probabilità di avere un infarto perché potrebbe accadere che chi mangia frutta tende anche a fare sport e magari è quella la causa del maggiore benessere e non il fatto di mangiare frutta!
Quando ci viene mostrata una statistica che presenta una correlazione tra due fenomeni dobbiamo allora esercitare un po’ di sano scetticismo, approfondire la questione e cercare di capire quale potrebbe essere il meccanismo di causa-effetto tra i due fenomeni. Se non si riesce a trovare una spiegazione convincente bisogna sempre considerare la possibilità che non vi sia alcun rapporto causale tra le due variabili.
L’argomento di questo articolo potrebbe essere usato nell’ambito dell’educazione civica con l’idea di sviluppare un maggiore senso critico sulle notizie che si leggono sui giornali.
Si potrebbero anche svolgere alcune attività, per esempio:
- immaginare altri casi in cui ci sia una correlazione ma non sia presente alcun rapporto di causa-effetto tra i due fenomeni;
- far cercare articoli dove vengono riportate statistiche che mostrano correlazioni tra grandezze e in seguito discutere con gli studenti se il rapporto di causa-effetto è verosimile o no.
